
- •Физические основы классической механики
- •I. Механика. Общие понятия
- •2. Кинематика точки
- •3. Скорость
- •4. Ускорение
- •5. Примеры
- •I. Основные понятия
- •2. Законы механики
- •3. Инерциальные системы отсчёта (и.С.О.)
- •4. Принципы относительности Галилея
- •5. Закон сохранения импульса
- •6. Реактивное движение
- •7. Центр инерции
- •I. Работа
- •2. Энергия
- •3. Кинетическая и потенциальная энергии
- •4. Закон сохранения механической энергии
- •5. Удар абсолютно упругих и неупругих тел
- •I. Кинематика вращательного движения
- •2. Кинетическая энергия вращательного движения. Момент инерции.
- •3. Основное уравнение динамики вращательного движения
- •4. Момент импульса. Закон сохранения момента импульса
- •I. Принцип относительности
- •2. Постулаты Эйнштейна
- •3. Преобразования Лоренца
- •4. Замедление времени
- •5. Сокращение длин
- •6. Сложение скоростей в теории относительности.
- •7. Изменение массы со скоростью
- •8. Движение релятивистской частицы
- •9. Связь между массой и энергией
- •10. Кинетическая энергия. Энергия и импульс
- •Колебания и волны
- •1. Общие сведения о колебаниях
- •2. Механические колебания
- •3. Энергия гармонических колебаний
- •1. Предмет молекулярной физики
- •2. Термодинамические параметры.
- •3. Идеальный газ
- •4. Основное уравнение мкт газов для давления.
- •5. Газовые законы как следствие молекулярно-кинетической теории.
- •1. Скорости теплового движения молекул
- •2. Распределение молекул по скоростям (Закон Максвелла)
- •3. Закон распределения Больцмана
- •4. Число столкновений и средняя длина свободного пробега молекул
- •1. Внутренняя энергия идеального газа
- •2. Первое начало термодинамики
- •3. Работа при расширении газа
- •4. Теплоемкость идеальных газов
- •5. Адиабатический процесс
- •1. Характеристика тепловых процессов.
- •2. Принцип действия тепловой машины
- •3. Второе начало термодинамики
- •1. Энтропия
- •1. Отклонение свойств газов от идеальных.
- •2. Уравнение состояния реального газа (уравнение Ван-дер-Ваальса)
- •1. Критическое состояние вещества
- •1. Внутренняя энергия реального газа
- •1. Жидкости.
- •2. Поверхностное натяжение.
- •3. Явление смачивания.
- •4. Формула Лапласа.
- •5. Капиллярность.
3. Идеальный газ
Наиболее простыми свойствами, которые можно описать уравнением состояния, обладает газ, находящийся в таких условиях, что взаимодействие между эго молекулами можно не учитывать. Такой газ, у которого молекулы можно принять за материальные точки и можно пренебречь их размерами и силами взаимодействия между ними, называют идеальным. Столкновения между молекулами такого газа происходят как столкновения упругих шаров.
4. Основное уравнение мкт газов для давления.
В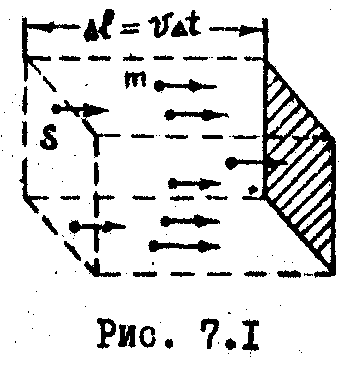 ыведем
уравнение состояния идеального газа.
Для этого вычислим давление потока
молекул упруго соударяющихся со стенкой
(Рис. 7.1).
ыведем
уравнение состояния идеального газа.
Для этого вычислим давление потока
молекул упруго соударяющихся со стенкой
(Рис. 7.1).
За время
![]() к стенке подойдут молекулы, содержащиеся
в объема
к стенке подойдут молекулы, содержащиеся
в объема
![]() воли их концентрация
воли их концентрация
![]() ,
то за время
о стенку ударится
,
то за время
о стенку ударится
![]() молекул:
молекул:
![]() (7.3)
(7.3)
При ударе о стенку на молекулу действует
сила![]() ,
в свою очередь по 3-му закону Ньютона
молекула действует на стенку с силой
,
в свою очередь по 3-му закону Ньютона
молекула действует на стенку с силой![]() ,
а все
молекул действуют с силой
:
,
а все
молекул действуют с силой
:
![]() (7.4)
(7.4)
Так как при упругом ударе меняется лишь
направление скорости на противоположное,
то
![]() и
и
![]() (7.5)
(7.5)
Подставив это в (7.4), получим
![]() .
.
так как давление
![]() ,
то
,
то
![]() (7.6)
(7.6)
В это выражение надо внести поправки.
Поскольку движение молекул газа
хаотично, то в заданном направлении
будет двигаться 1/6 их часть, и вместо
надо взять 1/6
, далее, так как из-за столкновений
скорости молекул различны, то вместо
квадрата скорости
![]() надо взять средний квадрат скорости:
надо взять средний квадрат скорости:
![]() (7.7)
(7.7)
С учетом этого получаем вместо (7.6):
![]() (7.8)
(7.8)
Учитывая, что
![]() ,
можно также записать:
,
можно также записать:
![]() (7.9)
(7.9)
Используя из определения температуры формулу (7.2), получим окончательно:
![]() или
или
![]() (7.10)
(7.10)
Это уравнение называют основным уравнением МКТ. Оно имеет универсальный характер, т.к. не зависит от природы газа.
5. Газовые законы как следствие молекулярно-кинетической теории.
Закон Авогадро. Запишем для двух:
газов уравнения (7.10) при одинаковых
![]() и
,
занимающих одинаковые объемы.
и
,
занимающих одинаковые объемы.
![]() ;
;![]() .
Отсюда следует
.
Отсюда следует
![]() ,
т.е. в одинаковых объемах при одинаковых
и
содержится одинаковое число молекул.
,
т.е. в одинаковых объемах при одинаковых
и
содержится одинаковое число молекул.
Число молекул в объеме одного моля
называется числом Авогадро
![]() .
Оно равно
.
Оно равно
![]() 1/моль.
1/моль.
Уравнение Менделеева-Клапейрона.
Число молекул
в газа можно записать как
![]() ,
где
- масса газа;
,
где
- масса газа;
![]() - молекулярная масса;
- молекулярная масса;
![]() - число молей. Тогда уравнение состояния
будет:
- число молей. Тогда уравнение состояния
будет:
![]() , (7.11)
, (7.11)
где
![]() - газовая постоянная. Используя значения
и
,
найдем:
- газовая постоянная. Используя значения
и
,
найдем:
![]()
![]() (7.12)
(7.12)
При
![]() (7.11) получаем
(7.11) получаем
![]() - закон Бойля-Мариотта,
- закон Бойля-Мариотта,
при
![]() ;
при
;
при
![]() .
Если
.
Если
![]() - температура замерзания воды, а вместо
- температура замерзания воды, а вместо
![]() использовать
использовать
![]() ,
то записанные соотношения примут вид:
,
то записанные соотношения примут вид:
![]() при
при
![]() - закон Гей-Люссака и
- закон Гей-Люссака и
![]() при
при
![]() - закон Шарля.
- закон Шарля.
Закон Дальтона. Если имеем смесь
газов, то
![]() .
Так как молекулы каждой компоненты газа
занимают весь объем,
.
Так как молекулы каждой компоненты газа
занимают весь объем,
![]() и,
и,
![]() (7.13)
(7.13)
т.е. давление смеси газов равно сумме парциальных давлений.
Лекция 10 |
Распределение Максвелла для молекул идеального газа по скоростям и энергиям. |
|
Распределение Больцмана. Барометрическая формула. Опыт Перрена. |
