
- •Основы алгоритмизации и программирования, язык Си
- •Введение
- •Блок-схема алгоритма Общие требования к блок-схеме алгоритма
- •Линейные и разветвляющиеся процессы
- •Циклические процессы
- •Итерационные процессы
- •Комментарии
- •Типы данных
- •Данные целого типа
- •Данные вещественного типа
- •Модификатор const
- •Переменные перечисляемого типа
- •Константы
- •Операции и выражения
- •Операция присваивания
- •Арифметические операции
- •Операции поразрядной арифметики
- •Логические операции
- •Операции отношения
- •Инкрементные и декрементные операции
- •Операция sizeof
- •Порядок выполнения операций
- •Приоритет операций
- •Преобразование типов
- •Операция приведения
- •Операция запятая
- •Ввод и вывод информации
- •Директивы препроцессора Директива #include
- •Директива #define
- •Понятие пустого и составного операторов
- •Условные операторы
- •Операторы организации цикла
- •Оператор цикла for
- •Оператор цикла while
- •Оператор цикла do … while
- •Вложенные циклы
- •Операторы перехода (break, continue, return, goto)
- •Примеры программ
- •Массивы Одномерные массивы
- •Примеры программ
- •Многомерные массивы (матрицы)
- •Примеры программ
- •Указатели Понятие указателя
- •Описание указателей
- •Операции с указателями
- •Связь между указателями и массивами
- •Массивы указателей
- •Многоуровневые указатели
- •Примеры программ
- •Символьные строки
- •Ввод/вывод строк.
- •Функции работы со строками.
- •Примеры программ
- •Функции
- •Прототип функции.
- •Определение функции.
- •Параметры функции
- •Параметры по умолчанию
- •Передача массива в функцию
- •Inline функции
- •Класс памяти
- •Автоматические переменные
- •Статические переменные
- •Регистровые переменные
- •Блочная структура
- •Примеры программ
- •Указатели на функции
- •Примеры программ
- •Рекурсия
- •Примеры программ
- •Аргументы в командной строке
- •Функции с переменным числом параметров
- •Примеры программ
- •Сортировка
- •Пузырьковая сортировка.
- •Шейкер сортировка
- •Сортировка вставкой
- •Сортировка выбором
- •Метод Шелла
- •Метод Хора
- •Структуры
- •Доступ к элементам структуры
- •Инициализация структур
- •Указатели на структуры.
- •Структуры и функции
- •Примеры программ
- •Поля бит
- •Объединения
- •Переменные с изменяемой структурой
- •Примеры программ
- •Организация списков и их обработка
- •Операции со списками при связном хранении
- •Построение обратной польской записи
- •Односвязный линейный список, очередь
- •Двусвязный линейный список
- •Циклический список, кольцо
- •Двусвязный циклический список
- •Примеры программ
- •Деревья
- •Потоки и файлы
- •Файлы Основные сведения о файловой системе
- •Организация посимвольного ввода и вывода
- •Определение конца файла feof()
- •Организация ввода и вывода строк
- •Удаление файлов
- •Дозапись потока
- •Позиционирование в файле
- •Текстовые и двоичные файлы
- •Функции fread() и fwrite()
- •Примеры программ
- •Хеширование
- •Схемы хеширования
- •Метод открытой адресации с линейным опробыванием
- •Метод цепочек
- •Машинное представление графов
- •Примеры программ
- •Литература
Блок-схема алгоритма Общие требования к блок-схеме алгоритма
Выбранный метод решения задачи необходимо привести к виду, удобному для записи программы. Такой промежуточной формой между формальной записью и записью в виде программы на алгоритмическом языке является блок- схема. Каждой программе (функции) должна соответствовать отдельная блок-схема алгоритма. При создании блок-схем необходимо учитывать требования ГОСТ 19.002-80 и ГОСТ 19.002-80.
Согласно этим ГОСТ, все размеры фигур связаны с двумя величинами: a и b, где a – величина, кратная 5, а b вычисляется по формуле b=1,5a, допускается b=2a. В 1992 года введен новый ГОСТ 19-701-90. Он описывает, как и где следует использовать фигуры. Схемы алгоритмов состоят из имеющих заданное значение символов (рис. 1), краткого пояснительного текста и соединяющих линий.
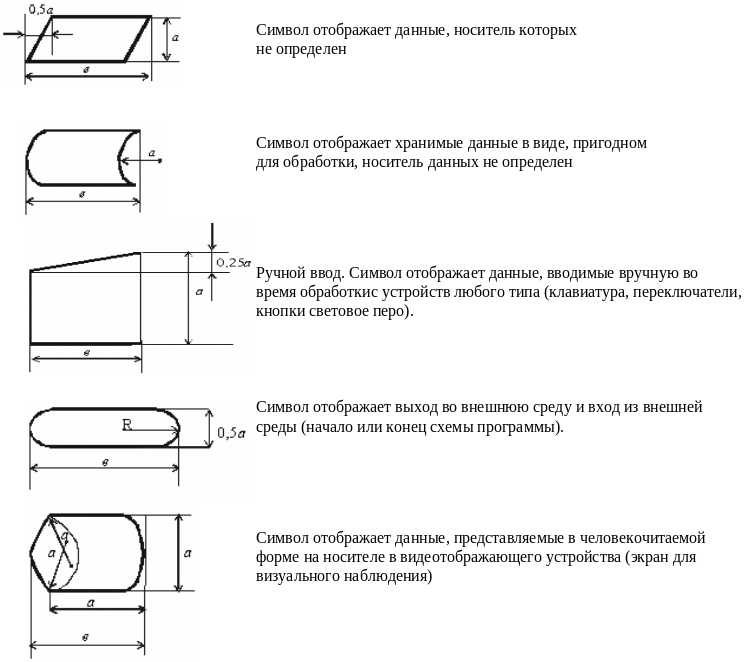

Рис. 1. Описание символов
Линейные и разветвляющиеся процессы
Вычислительный процесс называется линейным, если направление его продолжения на любом этапе вычислений является единственным. Алгоритм линейного вычислительного процесса описывает действия, последовательность выполнения которых не зависит от исходных данных и результатов промежуточных вычислений. Линейный процесс (как и любой другой вычислительный процесс) можно представить в виде следующих этапов:
задание исходных данных;
реализация вычислений
вывод результатов вычислений..
Пример: разработать блок-схему вывода значений функции y=ax+b. Значение аргументов а, b, x ввести с клавиатуры (рис. 2).

Рис. 2. Блок-схема линейного процесса
Разветвляющимся вычислительным процессом называется процесс, который в зависимости от исходных данных и результатов промежуточных вычислений осуществляется по одному из нескольких возможных вариантов направлений. Направления, по которым может выполняться вычислительный процесс, называется ветвями. Следовательно, отличие разветвляющегося вычислительного процесса от линейного состоит в том, что на этапе вычислений процесс может быть реализован по двум и более ветвям. При этом выбор направления (ветви) зависит от некоторого условия. Если условие выполняется, то выбирается одна ветвь иначе другая. Условие, определяющее выбор некоторой ветви алгоритма (вычислений), может быть сложным и состоять из нескольких простых условий. Выбор направления вычисления в этом случае осуществляется последовательной проверкой этих простых условий.
Пример . Разработать блок-схему нахождения корней квадратного уравнения ax2+bx+c=0. Значение коэффициентов а, b, c ввести с клавиатуры (рис. 3.).

Рис. 3. Блок-схема алгоритма нахождения корней уравнения.
Пример . Разработать блок-схему разветвляющегося вычислительного процесса для решения системы функций.
(a+2.3)/(b-1) , a-b≥0
y=
(a-b)/a , a-b<0
Значение коэффициентов а и b ввести с клавиатуры (рис. 4).
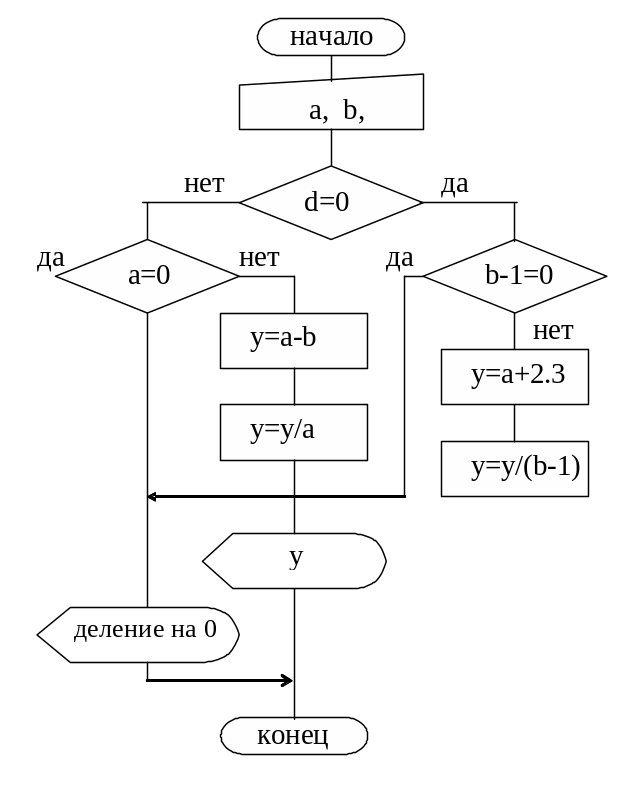
Рис. 4. Блок-схема алгоритма решения системы функций
Циклические процессы
В большинстве задач, встречающихся на практике, вычисления по некоторой группе формул необходимо выполнять многократно. Например, вычислить значение функции в заданных точках отрезка. Этот многократно повторяющийся участок вычислительного процесса называют циклом. Таким образом, под циклом понимается оператор или группа операторов, повторяющихся некоторое количество раз. Каждый проход по телу цикла называется итерацией.
Цикл, не содержащий внутри себя других циклов, называют простым, если он содержит внутри себя другие циклы или разветвления, то цикл называют сложным. Обычно при каждом повторении цикла вычисления осуществляются с новыми значениями переменных. В любом циклическом процессе в ходе вычислений необходимо решать вопрос: повторять вычисления или нет? Ответ на этот вопрос получают в результате анализа значений одной или нескольких переменных, т.е. анализа некоторого условия. Анализируемую переменную называют параметром цикла. Из выше изложенного следует, что циклический процесс является разветвляющимся процессом с двумя ветвями, из которых одна возвращается на предыдущие блоки, т.е. реализует цикл..
Блок-схема циклического процесса должна содержать блоки:
задания начального значения параметру цикла;
блок реализации необходимых вычислений;
блок изменения параметра цикла;
блок проверки условия окончания цикла.
Во многих задачах встречаются так называемые циклы по простой переменной. В этом случае задается начальное значение переменной, закон (правило) ее изменения и конечное значение переменной. В процессе решения задачи текущее значение переменной каждый раз сравнивается с конечным, и если переменная достигла конечного значения, то осуществляется выход из цикла.
Пример . Разработать блок-схему вывода значений функции y=x2+a, выбрать n значений аргумента х. Значение аргументов а, x, n ввести с клавиатуры, шаг аргумента x равен 0,25.

 Рис 5. Блок-схема циклического
алгоритма по простой переменной.
Рис 5. Блок-схема циклического
алгоритма по простой переменной.
В некоторых задачах невозможно указать закон получения следующего значения переменной. В этом случае значение переменной цикла вводится из входного потока (клавиатуры).
Пример . Разработать блок-схему ввода с клавиатуры чисел в массив (ввод закончить при вводе числа 99), и вычисления max значения в массиве.

Рис 6. Блок-схема циклического процесса.
Если требуется вычислить, например, сумму некоторых чисел, то переменной используемой для накопления результата перед циклом необходимо присвоить нулевое значение или значение первого слагаемого. Иначе конечный результат может быть не определен (иметь любое значение).
