4.5.2. Умови рівноваги системи пар сил

Враховуючи властивості рівнодійної збіжних сил, результуючої пари сил, властивості вектора моменту пари сил як вільного вектора, а також умови рівноваги збіжної системи сил, отримаємо наступні необхідні й достатні умови рівноваги тіла під дією системи пар сил :

- векторна (геометрична) форма рівноваги:

, (4.11)

тобто многокутник моментів пар сил початкової системи (рис. 4.12) повинен бути замкненим: кінець останнього вектора повинен збігатися з початком (точкою О) першого;

- аналітична (алгебраїчна) форма рівноваги:

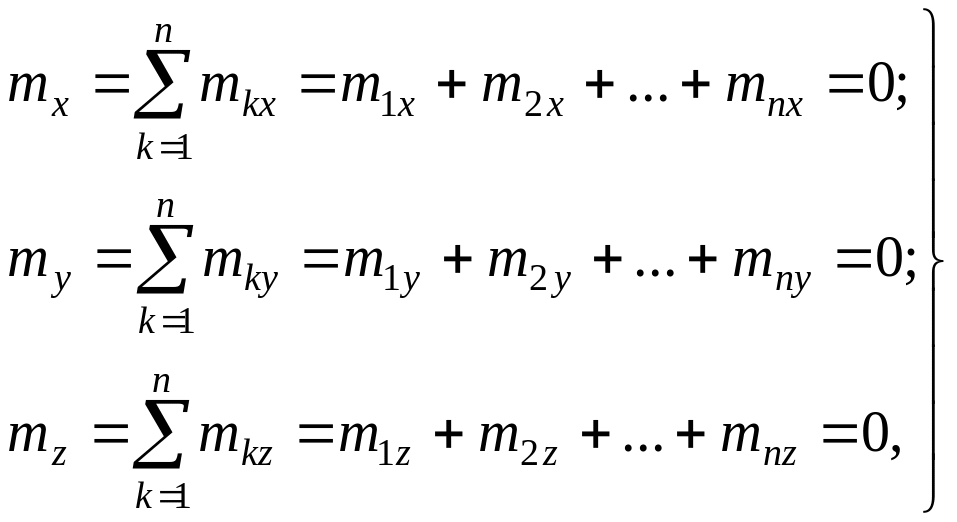(4.12)

тобто суми проекцій моментів пар сил системи на кожну з трьох координатних осей дорівнюватимуть нулю.

5. Довільна система сил у просторі й площині. Приведення до заданого центра (теорема пуансо)

У реальних умовах експлуатації на тіло, нехай-то електродвигун, кузов трамваю, лопатка турбіни, гребля, каркас будинку чи ін., діє система зовнішніх сил.

Існує декілька типових систем сил, що використовуються в розрахунках на практиці. Це довільна система сил у просторі, довільна система сил у площині, система паралельних сил і будь-яка їх комбінація.

Цей розділ присвячено питанням приведення вихідної системи сил у про-сторі й площині до найпростішого вигляду в загальному і окремих випадках.

5.1. Лема про паралельне перенесення сили

Відповідно до аксіоми 2 статики (див. розд. 1) прикладену до тіла силу можна переносити вздовж її лінії дії в будь-яку іншу його точку. При цьому дія сили на тіло, а також стан тіла не змінюються.

У ряді практичних задач рівноваги, пов’язаних зі спрощенням заданої системи сил, часто виникає необхідність перенесення сили до заданого центра паралельно самій до себе.

На відміну від попереднього випадку паралельне перенесення сили призводить в умовах збереження початкового механічного стану тіла до зміни системи діючих на нього силових факторів: до тіла необхідно додатково додати пару сил, параметри якої визначає наступна лема.

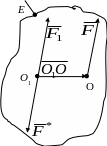
Лема. Прикладену до тіла в точці О (рис. 5.1,а) силу можна перенести паралельно самій собі в будь-яку його іншу точку О₁ (центр приведення), додаючи при цьому, для збереження механічного стану тіла, пару сил з моментом , рівним моменту вихідної сили відносно центра приведення О₁.

а б

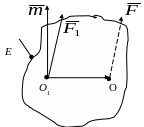
в

Рис. 5.1

Доведення. Нехай у точці О (рис. 5.1,а) до тіла прикладена розташована в площині Е сила . Позначимо систему сил, діючу на тіло, як ( ). Виберемо в тілі, в пл. Е, довільну точку О₁, положення якої визначимо вектором . Позначимо її як центр приведення “О₁”. Прикладемо далі в пл. Е у цьому центрі (рис. 5.1,б) еквівалентну нулю систему двох сил (двійку сил) з параметрами: . При цьому, відповідно до аксіоми 2 статики, стан тіла не зміниться, а вихідна система сил ( ) перетвориться в еквівалентну систему трьох сил: .

За побудовою на рис. 5.1,б, сила прикладена в точці приведення О₁ і дорівнює , а система двох сил створює пару сил, що називається приєднаною парою сил. Далі в центрі приведення О₁ на рис. 5.1,в побудуємо вектор , рівний моменту отриманої пари сил, і вектор , рівний моменту вихідної сили відносно полюса О₁. За визначенням вони є перпендикулярними до пл. Е, прикладеними в точці О₁ і рівними. Тобто момент приєднаної пари сил дорівнює моменту вихідної сили відносно нового центра приведення О₁:

. (5.1)

Отже лему доведено.

Рівняння (5.1) використовують на практиці при визначенні параметрів приєднаної пари сил і сили , які в більшості випадків являють собою прикладений до ланки механізму крутний момент і силу тиску ланки на вісь.

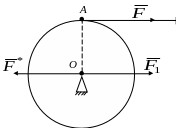
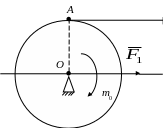Розглянемо, наприклад, барабан радіуса (рис. 5.2,а), до якого в точці А з боку намотаної нитки прикладено силу . Використуємо для сили доведену лему, прийнявши за центр приведення точку О. У результаті отримаємо, що вихідна система сил ( ) зводиться: до сили (рівній ) і до пари сил з моментом (рис. 5.2,а). При цьому на барабан діють: момент , який обертає барабан, і сила , що здійс-

R

а б

Рис. 5.2

нює тиск на вісь барабану (рис. 5.2,б). Їх величини використовуються в подальшому при розв’язанні задач динаміки і міцності системи “опора - вісь - барабан - нитка”.