7. Законы Ома и Кирхгофа в комплексной форме. Пример последовательной rlc - цепи.

Зная компл сопротивление (компл проводимость) участка цепи и одну из приложенных к данному участку цепи величин: ток или напряжение , можно найти неизвестное напряжение или неизвестный ток исследуемого участка

(2.29)

Аналогично комплексные действующие значения напряжения и тока на зажимах участка цепи (2.30)

Выражения (2.29), (2.30) являются математической записью закона Ома в комплексной форме.

Таким образом, комплексная схема замещения цепи может быть получена из эквивалентной схемы для мгновенных значений заменой всех идеализированных пассивных двухполюсников их комплексными сопротивлениями (проводимостями) и всех токов и напряжений – их комплексными изображениями.

Мгновенные значения токов и напряжений различных ветвей электрической цепи связаны между собой линейными алгебраическими уравнениями баланса токов и напряжений, составляемыми на основании законов Кирхгофа. Учитывая, что суммированию гармонических функций времени соответствует суммирование их комплексных изображений, перейдем от законов Кирхгофа для мгновенных значений токов и напряжений к законам Кирхгофа для комплексных изображений токов и напряжений, называемых обычно законами Кирхгофа в комплексной форме.

Первый закон Кирхгофа: сумма комплексных амплитуд (комплексных действующих значении) токов всех ветвей, подключенных к каждому из узлов электрической цепи, равна нулю:

(2.31)

Здесь - номер ветви, подключенной к рассматриваемому узлу.

Второй закон Кирхгофа в комплексной форме: сумма комплексных амплитуд (комплексных действующих значений) напряжений всех ветвей, входящих в любой контур моделирующей цепи, равна нулю:

(2.32)

Здесь – номер ветви, входящей в рассматриваемый контур.

В ряде случаев удобно использовать другую формулировку второго закона Кирхгофа в комплексной форме: сумма комплексных изображений напряжений на всех элементах любого контура моделирующей цепи равна, сумме комплексных изображений э. д. с., всех входящих в контур источников напряжения: (2.33) Здесь , - комплексные изображения напряжений всех элементов контура, за исключением источников напряжения; , - комплексные изображения э. д. с. источников напряжения, действующих в рассматриваемом контуре.

Последовательная RLC-цепь

Используя законы Ома и Кирхгофа в комплексной форме, составим систему уравнений электрического равновесии цепи

; ;

; ; (2.63)

. где ; ; - комплексные сопротивления входящих в цепь идеализированных элементов. Решая систему (2.63) относительно тока , получаем . (2.64) Здесь - комплексное входное сопротивление последовательной RLC-цепи, равное сумме комплексных сопротивлений входящих в цепь элементов, которое определяется только параметрами входящих в цепь элементов и частотой внешнего воздействия: . (2.65)

Рис. 2.15. Векторные диаграммы для тока и напряжений последовательной RLC-цепи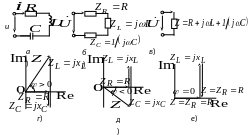

Переходя от алгебраической формы записи к показательной, находим модуль и аргумент комплексного входного сопротивления: ; ; (2.66)

Из выражения (2.66) следует, что характер входного сопротивления цепи зависит от соотношения между мнимыми составляющими комплексного входного сопротивления ёмкости и индуктивности . При входное сопротивление цепи имеет резистивно-индуктивный характер ( ). Векторная диаграмма, построенная на основании выражения (2.65) и иллюстрирующая данный случай, представлена на рис. 2.14, г (для большей наглядности векторы и изображены немного смещенными один относительно другого). Если , то входное сопротивление цепи имеет резистивно-емкостной характер ( ) (рис. 2.14, д). При мнимые составляющие входного сопротивления емкости и индуктивности взаимно компенсируются и входное сопротивление цепи имеет чисто резистивный характер ( )

И спользуя уравнение (2.64), можно по известному напряжению, приложенному к внешним зажимам цепи, найти ток и наоборот (рис.2.15).

Падение напряжения на сопротивлении , совпадает по направлению с током ; напряжение сдвинуто по фазе относительно на (опережает ток); напряжение отстает по фазе от тока на и направлено в противоположную сторону . При сумма совпадает по направлению с вектором , ток цепи отстает по фазе от напряжения ( ) При сумма совпадает по направлению с вектором , ток цепи опережает по фазе напряжение ( ) Если , то сумма , напряжение на зажимах цепи равно напряжению на сопротивлении , ток цепи совпадает по фазе с приложенным напряжением ( ).