Параллельное соединение связанных индуктивностей

При параллельном соединении связанных индуктивностей (рис. 5.4.) к их зажимам прикладывается одинаковое напряжение, а входной ток рассматриваемого участка цепи складывается из токов обеих индуктивностей:

i = i₁ + i₂.

Рис. 5.4. Последовательное соединение связанных индуктивностей

Используя компонентные уравнения связанных индуктивностей (5.10), составляем систему уравнений:

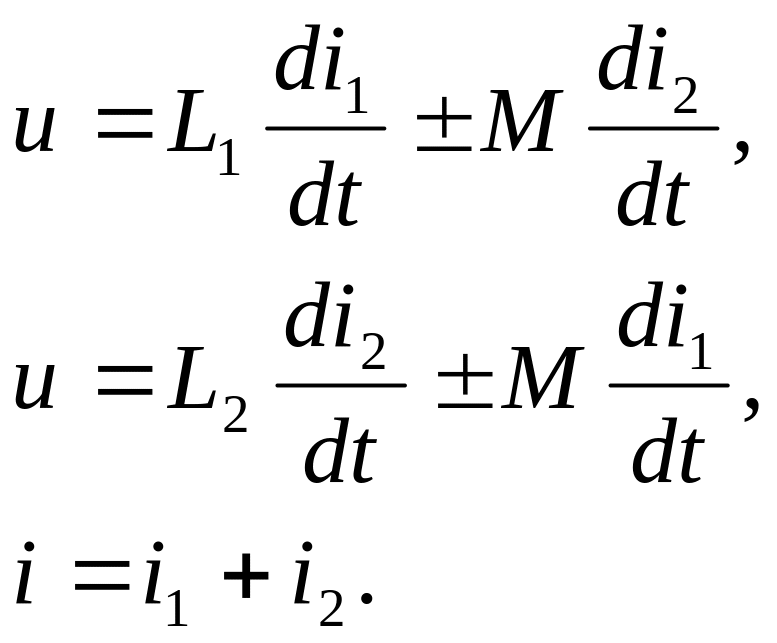
Из решения системы находим зависимость между напряжением и током на зажимах рассматриваемого участка цепи:

Следовательно, участок цепи, представляющий собой две параллельно включенные связанные индуктивности, обладает эквивалентной индуктивностью

Знак минус соответствует согласному включению, а знак плюс — встречному.

Связанные индуктивности с одной общей точкой

Найдем схему замещения участка цепи, содержащего две связанные индуктивности, включенные таким образом, что они имеют одну общую точку(рис. 5.5).

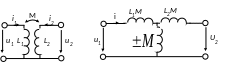
а) б)

Рис. 5.5. Cвязанные индуктивности с одной общей точкой и эквивалентная схема без связанных индуктивностей Преобразуем систему компонентных уравнений (5.10). Добавим и вычтем в первом уравнении , во втором уравнении : 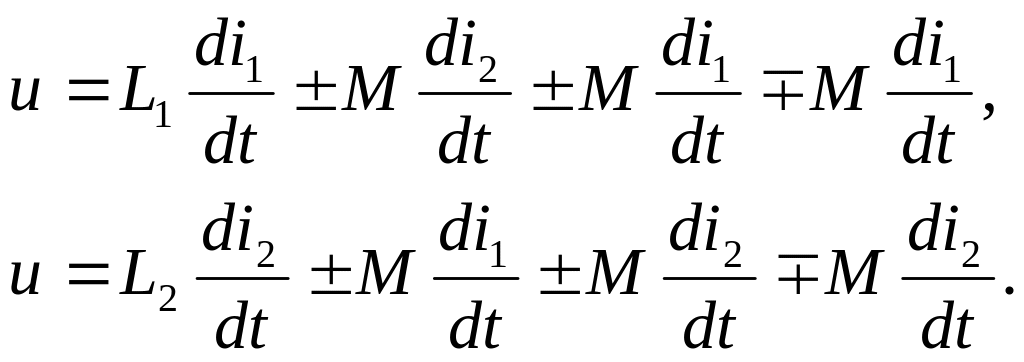После преобразований имеем: 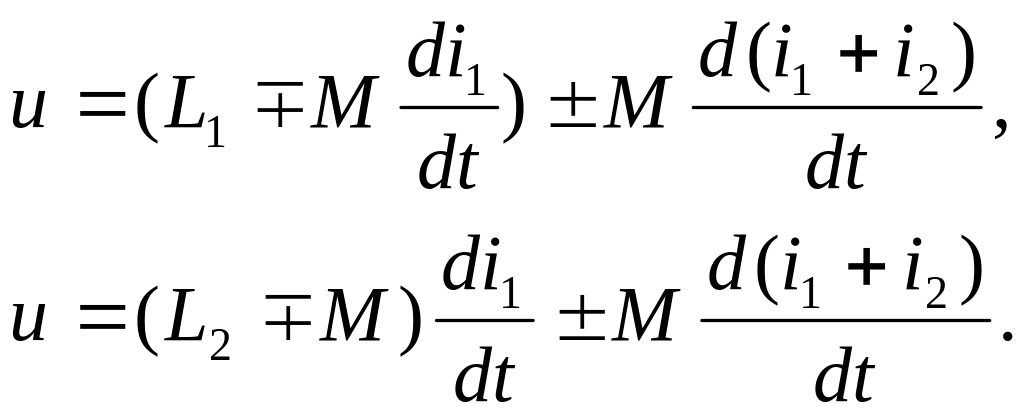(5.17)Здесь, как и в полученных ранее выражениях, верхний знак соответствует согласному, а нижний знак — встречному включению связанных индуктивностей.

26.Резонанс в системе связанных контуров, резонансные частоты, фактор связи, ачх и фчх системы связанных контуров.

Резонанс – это такой режим работы электрической цепи, содержащей емкости и индуктивности, при котором реактивные составляющие входных сопротивления и проводимости цепи равны нулю.

Резонансная частота - частота внешнего воздействия, соответствующая фазовому резонансу. На резонансной частоте входные сопротивление и проводимость электрической цепи имеют чисто резистивный характер, а входной ток цепи совпадает по фазе с приложенным напряжением.

Фактор связи: Рассмотрим зависимость тока вторичного контура от частоты для случая, когда параметры обоих контуров одинаковы(х₁₁=х₂₂=х, r₁₁=r₂₂=r, ω₀₁=ω₀₂=ω, ρ₁=ρ₂= ρ, Q₁=Q₂=Q). Собственные сопротивления первичного и вторичного контуров при этом могут быть представлены в виде: Z₁₁=Z₂₂=r+jx=r(1+jξ). Исп. это и Z₁₂=jx₁₂ подставляем в выр-е получаем 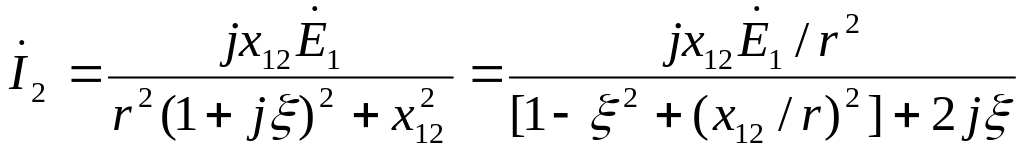, тогда , учитывая что E₁/2r –мах. зн-е тока вторичного тока, то , где -постоянный коэф, фактор связи.

Найдем экстремумы этой функции. приравниваем первую производную знаменателя к нулю, получаем ξ(ξ²+1-А)=0, ξ₁=0(это соответствует настройке контуров на индивидуальный резонанс, ω=ω₀), ξ_2,3= -это имеет смысл лишь тогда, когда А не меньше А_кр=1. Таким образом, при больших значения параметра связи(А>А_кр) у функции 3 экстремума(частотные характеристики имеют вид «двугорбых» кривых), а при малых-один(частотные хар-ки имеют вид «одногорбых» кривых). Таким образом, по сравнению с одиночными колебательными контурами связанные контуры обладают лучшими избирательными свойствами: АЧХ связанных контуров имеют форму, более близкую к прямоугольной, и хар-ся большой крутизной склонов за пределами полосы пропускания.

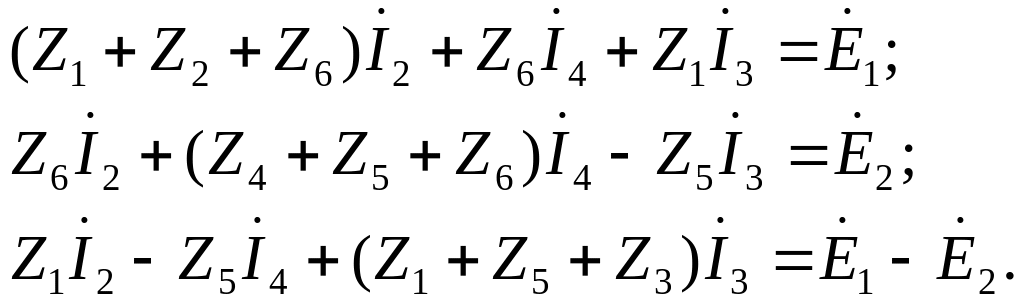Матрицы: