
- •1.Идеализированные и реальные элементы электрической цепи: сопротивление, емкость, индуктивность, их математические модели.
- •2.Классификация электрических цепей: линейные, нелинейные, параметрические цепи.
- •3. Законы Кирхгофа для мгновенных значений токов и напряжений
- •5) Энергия, мгновенная мощность, средняя мощность электрических колебаний.
- •6.Метод комплексных амплитуд. Ограничения на его применение.
- •7. Законы Ома и Кирхгофа в комплексной форме. Пример последовательной rlc - цепи.
- •8.Понятие о комплексных частотных характеристиках(кчх). Амплитудно-частотоные характеристики(ачх), фазо-частотные характеристики(фчх), годограф цепи.
- •11.Кчх последовательного колебательного контура, входное сопотивление, входная проводимость.
- •12. Избирательные свойства последовательного колебательного контура. Добротность, резонансная частота, полоса пропускания, связь между ними.
- •13. Параллельный колебательный контур. Разновидности параллельных
- •14) Комплексные частотные характеристики последовательного колебательного контура
- •16. Метод контурных токов в комплексной форме.
- •17.Метод узловых потенциалов. Определение числа независимых уравнений. Матричная запись системы уравнений. Полная матрица узлов (матрица инциденций). Примеры.
- •Теорема наложения (суперпозиции)
- •21. Линейный трансформатор при гармоническом воздействии.
- •22. Лин. Трансформатор при гармонич. Воздействии. Вывод ур-й эл. Равновесия в компл. Форме. Экв. Схема замещения трансформатора.
- •24.Система связанных контуров. Схемы замещения системы связанных контуров
- •25. Система индуктивно связанных контуров при гармоническом воздействии. Схемы замещения, вывод комплексных коэффициентов передачи по напряжению и по току.
- •Параллельное соединение связанных индуктивностей
- •26.Резонанс в системе связанных контуров, резонансные частоты, фактор связи, ачх и фчх системы связанных контуров.
- •29. Системы y и z параметров четырехполюсника. Связь между ними.
- •30. Уравнения четырехполюсника в форме а-параметров. Прямые и обратные постоянные четырехполюсника.
- •31. Системы уравнений четырехполюсника в форме h- и g-параметров, связь между ними.
- •34. Характеристические параметры симметричного пассивного четырехполюсника.
- •35.Комплексные частотные характеристики прямой и обратной передачи по току и напряжению. Связь между ними и характеристическими параметрами пассивного несимметричного четырехполюсника.
- •Вопрос 37. П- и т- образная эквивалентная схема замещения четырехпо-люсника.
- •Вопрос 38. Экспериментальное определение a-,z-,y- параметров через параметры холостого хода и короткого замыкания.
- •39. Основные уравнения многополюсника. Неопределенная матрица проводимостей и сопротивлений.
- •40(1). Треугольники сопротивлений и проводимостей. Преобразование треугольника в эквивалентную звезду. Преобразование звезды в эквивалентный треугольник.
- •40(2). Осн. Теоремы лин. Цепей: обратимости, компенсации, об эквивалентном источнике.
- •Вопрос 42. Модели реального конденсатора и катушки индуктивности при гармоническом воздействии. Добротность конденсатора и катушки индуктивности, их физический смысл.
- •Вопрос 41. Идеализированные реактивные элементы (индуктивность,
- •Емкость
- •Индуктивность
1.Идеализированные и реальные элементы электрической цепи: сопротивление, емкость, индуктивность, их математические модели.
С опротивление
- идеализированный пассивный элемент,
в котором электрическая энергия
необратимо преобразуется в какой-либо
другой вид энергии, например в тепловую,
механическую или световую. По свойствам
к идеализированному пассивному элементу
- сопротивлению наиболее близки резисторы
- реальные элементы электрической цепи,
в которых электрическая энергия в
основном преобразуется в тепловую.
Условное графическое обозначение
сопротивления приведено на Рис.
опротивление
- идеализированный пассивный элемент,
в котором электрическая энергия
необратимо преобразуется в какой-либо
другой вид энергии, например в тепловую,
механическую или световую. По свойствам
к идеализированному пассивному элементу
- сопротивлению наиболее близки резисторы
- реальные элементы электрической цепи,
в которых электрическая энергия в
основном преобразуется в тепловую.
Условное графическое обозначение
сопротивления приведено на Рис.
В
 ольт-амперная
характеристика резистора, т.е. зависимость
между значениями тока и напряжения на
его зажимах u=u(i)
или i=i(u),
в общем случае имеет нелинейный характер.
ольт-амперная
характеристика резистора, т.е. зависимость
между значениями тока и напряжения на
его зажимах u=u(i)
или i=i(u),
в общем случае имеет нелинейный характер.
Статическое сопротивление – это отношение мгновенных значений напряжения и тока на зажимах резистора:RСТ = uR /iR Динамическое сопротивление резистора определяется производной мгновенного значения напряжения на его зажимах по току:RДИН = duR /diR (1.8)
Зависимость между током и напряжением на зажимах линейного сопротивления подчиняется закону Ома, который можно записать в виде uR = RiR (1.9) или iR = GuR, (1.10) где G = 1/R – проводимость.
Е мкостью
называется идеализированный элемент
электрической цепи, обладающий свойством
запасать энергию электрического поля,
причем запасания энергии магнитного
поля или преобразования электрической
энергии в другие виды энергии в ней не
происходит. По свойствам к идеализированному
элементу - емкости - наиболее близки
реальные элементы - конденсаторы.
Условное графическое, обозначение
емкости приведено на рис.
мкостью
называется идеализированный элемент
электрической цепи, обладающий свойством
запасать энергию электрического поля,
причем запасания энергии магнитного
поля или преобразования электрической
энергии в другие виды энергии в ней не
происходит. По свойствам к идеализированному
элементу - емкости - наиболее близки
реальные элементы - конденсаторы.
Условное графическое, обозначение
емкости приведено на рис.
Зависимость заряда q, накопленного в емкости, от напряжения uC, называемая кулон-вольтной характеристикой, имеет в общем случае, нелинейный характер.
Количественно зависимость заряда, накопленного в емкости, от напряжения оценивают значениями статической и динамической емкостей: CСТ = q/u и CДИН = dq/duВ общем случае динамическая емкость не равна статической. Емкость, значение которой не зависит от напряжения, называется линейной; емкость, значение которой зависит от напряжения, - нелинейной. С = dq/duC = q/uC зависимость напряжения на емкости от тока:
Е![]() сли
uC
>
0
и убывает, т.е. dиC/dt
< 0,
то мгновенная мощность емкости
отрицательна. Емкость при этом разряжается,
т.е. отдает накопленную энергию во
внешнюю цепь.
сли
uC
>
0
и убывает, т.е. dиC/dt
< 0,
то мгновенная мощность емкости
отрицательна. Емкость при этом разряжается,
т.е. отдает накопленную энергию во
внешнюю цепь.
Э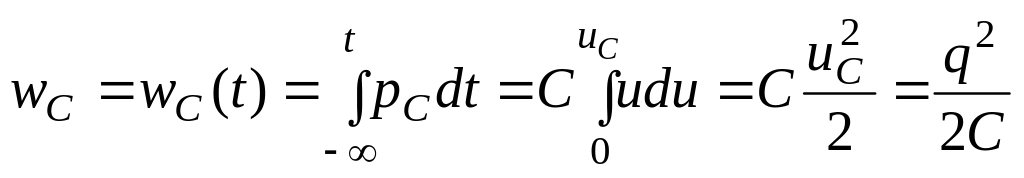 нергия
электрического поля, запасенная емкостью
в произвольный момент времени t,
определяется напряжением емкости или
ее зарядом:
нергия
электрического поля, запасенная емкостью
в произвольный момент времени t,
определяется напряжением емкости или
ее зарядом:
Очевидно, что в любой момент времени t энергия, запасенная в емкости, будет неотрицательной величиной.
И ндуктивностью
называется идеализированный элемент
электрической цепи, в котором происходит
запасание энергии магнитного поля.
Запасания энергии электрического поля
или преобразования электрической
энергии в другие виды энергии в ней не
происходит. Наиболее близким к
идеализированному элементу - индуктивности
- является реальный элемент электрической
цепи - индуктивная катушка. В отличие
от индуктивности в индуктивной катушке
имеют место также запасание энергии
электрического поля и преобразование
электрической энергии в другие виды
энергии, в частности в тепловую.
Количественно способность реального
и идеализированного элементов
электрической цепи запасать энергию
магнитного поля характеризуется
параметром, называемым индуктивностью.
ндуктивностью
называется идеализированный элемент
электрической цепи, в котором происходит
запасание энергии магнитного поля.
Запасания энергии электрического поля
или преобразования электрической
энергии в другие виды энергии в ней не
происходит. Наиболее близким к
идеализированному элементу - индуктивности
- является реальный элемент электрической
цепи - индуктивная катушка. В отличие
от индуктивности в индуктивной катушке
имеют место также запасание энергии
электрического поля и преобразование
электрической энергии в другие виды
энергии, в частности в тепловую.
Количественно способность реального
и идеализированного элементов
электрической цепи запасать энергию
магнитного поля характеризуется
параметром, называемым индуктивностью.
Условное графическое обозначение индуктивности приведено на рис.
Связь между напряжением и током в индуктивной катушке определяется законом электромагнитной индукции, из которого следует, что при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится электродвижущая сила е, пропорциональная скорости изменения потокосцепления катушки Ψ и направленная таким образом, чтобы вызываемый ею ток стремился воспрепятствовать изменению магнитного потока:
П![]()
![]() отокосцепление
катушки равно алгебраической сумме
магнитных потоков Φi,
пронизывающих ее отдельные витки:
отокосцепление
катушки равно алгебраической сумме
магнитных потоков Φi,
пронизывающих ее отдельные витки:
где N - число витков катушки.
Потокосцепление катушки Ψ, так же как и магнитный ноток Φ, может быть представлено в виде суммы двух составляющих: потокосцепления самоиндукции ΨСИ , и потокосцепления внешних полей ΨВП. Наведенная в индуктивной катушке э.д.с. е, в свою очередь, может быть представлена в виде суммы э.д.с. самоиндукции, которая вызвана изменением магнитного потока самоиндукции, и э.д.с., вызванной изменением магнитного потока внешних по отношению к катушке полей. Количественно зависимость потокосцепления самоиндукции от тока определяется статической LСТ и динамической LДИН индуктивностями катушки:
![]()
При анализе цепей обычно рассматривают не значение э.д.с., наведенной в катушке, а напряжение uL:
![]()
Энергия, запасенная в индуктивности в произвольный момент времени t:
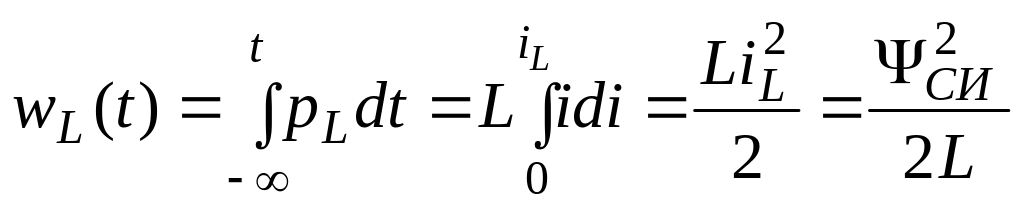
Таким образом, энергия, запасенная в индуктивности, является неотрицательной величиной и определяется только током индуктивности или потокосцеплением самоиндукции.
Идеализированные элементы электрической цепи (емкость и индуктивность), способные запасать энергию электрического или магнитного полей, называются энергоемкими или реактивными.
