28. Представление чисел в формате с фиксированной и с плавающей запятой.
Число с плавающей запятой это синоним числа, записанного в экспоненциальной форме. Формула записи:
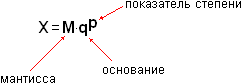
То, что таким образом можно записать любое число достаточно очевидно, хотя бы потому, что обычное представление это частный случай экспоненциального – когда показатель степени равен 0. Дальше, несложно заметить, что такое представление не однозначно: мы можем делить/умножать мантиссу на основание, соответственно меняя показатель степени.
1,23 *105 = 12,3 * 104 = 1230 * 102 = 0,123 * 106 = 1230000 * 10-1 |
В вычислительных машинах показатель степени принято отделять от мантиссы буквой «E» (exponent). Например, число 1,528535047×10−25 в большинстве языков программирования высокого уровня записывается как 1.528535047E-25.
Нормальной
формой числа
с плавающей запятой называется такая
форма, в которой мантисса находится на
полуинтервале [0; 1) (
).
Число с плавающей запятой, находящееся
не в нормальной
форме,
теряет точность по сравнению с нормальной
формой. Такая
форма записи имеет недостаток: некоторые
числа записываются неоднозначно
(например, 0,0001 можно записать в 4 формах —
0,0001×100,
0,001×10−1,
0,01×10−2,
0,1×10−3),
поэтому распространена также другая
форма записи — нормализованная,
в которой мантисса десятичного числа
принимает значения от 1 (включительно)
до 10 (не включительно), а мантисса
двоичного числа принимает значения от
1 (включительно) до 2 (не включительно)
(
).
В такой форме любое число (кроме 0)
записывается единственным образом.
Недостаток заключается в том, что в
таком виде невозможно представить 0,
поэтому представление чисел в информатике
предусматривает специальный признак
(бит)
для числа 0.
Число с фиксированной запятой — формат представления вещественного числа в памяти ЭВМ в виде целого числа. При этом само число x и его целочисленное представление x′ связаны формулой
,
где z —
цена (вес) младшего разряда.
В
случае, если z <
1,
для удобства расчётов делают, чтобы
целые числа кодировались без погрешности.
Другими словами, выбирают целое
число u (машинную
единицу)
и принимают 
.
В случае, если z >
1,
его делают целым.
Немногие языки программирования предоставляют встроенную поддержку чисел с фиксированной запятой, поскольку для большинства применений двоичное или десятичное представление чисел с плавающей запятой проще и достаточно точно. Числа с плавающей запятой проще из-за их большего динамического диапазона, для них не нужно предварительно задавать количество цифр после запятой. Если же потребуется арифметика с фиксированной запятой, она может быть реализована программистом даже на языках типа C и C++, которые обычно не включают в себя такой арифметики.