29. Производная функции, ее геометрический и физический смысл. Связь между непрерывностью и дифференцируемостью функции.

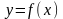Определение 1. Число называется производной функции в точке , если существует предел (т.е. производной функции в точке называется предел отношения приращения функции 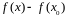в точке к вызвавшему его приращению аргумента при условии, что : ).

Производная обозначается как или как .

Определение 2. Касательной к графику функции в точке называют предельное положение секущей при .

Так как ,то уравнение касательной имеет вид

Геометрический смысл производной состоит в том, что она является угловым коэффициентом касательной к графику функции в точке .Определение 3. Если функция имеет производную в некоторой точке, то она называется дифференцируемой в этой точке. Процесс нахождения производной называется дифференцированием функции.Определение 4. Функция называется дифференцируемой в интервале (a;b), если она дифференцируема в каждой точке этого интервала. Теорема 1. Если функция дифференцируема в некоторой точке, то она в этой точке непрерывна.

30. Правила нахождения производной: производная произведения и производная частного.

31. Производная сложной и обратной функции.Теорема 6. Если функция имеет производную в точке , а функция имеет производную 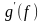в соответствующей точке , то сложная функция в данной точке имеет производную 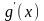, которая находится по формуле или

.

Теорема 5. Пусть функция монотонна в некотором интервале и имеет в некоторой точке этого интервала производную . Тогда в соответствующей точке обратная функция имеет производную , причем

.

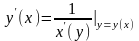32. Производные основных элементарных функций.

	­

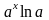
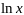
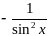
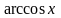
34. Логарифмическая производная.

Определение 1. Операция, состоящая в последовательном применении к равенству сначала логарифмирования, а затем дифференцирования, называется логарифмическим дифференцированием, а соответствующая производная – логарифмической производной.С помощью логарифмического дифференцирования, выведем формулу . Действительно, .

Производная показательно-степенной функции. Пусть и – дифференцируемые функции. Тогда функция называется показательно степенной. Найдем ее производную, для этого прологарифмируем тождество , а затем найдем производную от правой и левой части: , , т.е. имеем формулу .