- •1.Матрицы и действия над ними. Умножение матриц.
- •4. Обратная матрица и ее вычисление.
- •5. Система линейных уравнений. Формулы Крамера.
- •6) Матричный метод решения системы уравнений. Метод Гаусса.
- •8. Скалярное произведение векторов и его свойства. Угол между двумя векторами в координатной форме. Условие ортогональности двух векторов.
- •9. Векторное произведение двух векторов, его свойства и геометрический смысл.
- •2. Свойства векторного произведения.
- •10. Смешанное произведение трех векторов и его геометрический смысл. Условие компланарности векторов.
- •4. Свойства смешанного произведения.
- •11. Параметрическое и каноническое уравнения прямой на плоскости.
- •16. Уравнения линий на плоскости. Кривые второго порядка: окружность и эллипс.
- •17. Гипербола и ее каноническое уравнение.
- •18. Парабола и ее каноническое уравнение.
- •19. Полярные координаты на плоскости. Связь между полярными и декартовыми координатами.
- •20. Функция. Способы задания функции. Основные характеристики функции.
- •Определение 1. Абсолютной величиной или модулем действительного числа называется само это число, если и число , если :
- •22. Числовая последовательность и ее предел. Сходимость числовой последовательности.
- •23. Предел функции в точке, предел функции в бесконечности. Бесконечно малые функции. Предел монотонных функций.
- •24. Первый замечательный предел.
- •25. Второй замечательный предел.
- •27. Точки разрывов, их классификация.
- •28. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.
- •29. Производная функции, ее геометрический и физический смысл. Связь между непрерывностью и дифференцируемостью функции.
- •30. Правила нахождения производной: производная произведения и производная частного.
- •32. Производные основных элементарных функций.
- •34. Логарифмическая производная.
- •35. Дифференцирование функций, заданных в параметрической форме. Неявная функция и ее производная.
- •36. Дифференциал функции, его свойства и геометрический смысл. Производные высших порядков.
- •37. Теорема Ферма и теорема Ролля.
- •38. Теорема Лагранжа и теорема Коши.
- •39. Правило Лопиталя раскрытия неопределенностей.
18. Парабола и ее каноническое уравнение.
Определение
4.
Параболой
называется множество всех точек
плоскости, равноудаленных от данной
точки
 этой плоскости, называемой фокусом, и
данной прямой
этой плоскости, называемой фокусом, и
данной прямой
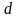 ,
называемой директрисой
(
,
называемой директрисой
(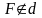 ).
).
Пусть
расстояние между фокусом
и директрисой
равно
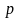 .
Эта величина называется параметром
параболы.
.
Эта величина называется параметром
параболы.
Уравнение параболы имеет вид
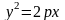
19. Полярные координаты на плоскости. Связь между полярными и декартовыми координатами.
Полярная система
координат на плоскости определяется
заданием некоторой точки О, луча
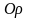 ,
исходящего из этой точки, и единицы
масштаба. Точка О называется полюсом,
а луч
- полярной
осью.
,
исходящего из этой точки, и единицы
масштаба. Точка О называется полюсом,
а луч
- полярной
осью.
М

О
Пусть М – произвольная точка плоскости. Обозначим через ее расстояние от полюса и через угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ. Числа и называются полярными координатами точки М, при чем величина называется полярным радиусом, а - полярным углом точки М.
По своему определению
величина
неотрицательная ( ).
Если ограничить изменение угла
пределами
).
Если ограничить изменение угла
пределами
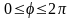
то
каждой точке плоскости однозначно
отвечает пара чисел
 .
.
20. Функция. Способы задания функции. Основные характеристики функции.
Отрезок
(сегмент)
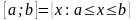 .
.
Интервал
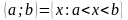 .
.
Полуинтервал
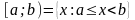 ,
,

Определение 1. Абсолютной величиной или модулем действительного числа называется само это число, если и число , если :
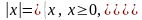
Свойства
модуля действительного числа: 1)
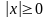 ,
2)
,
2)
 ,
3)
,
3)
 ,
если
,
если
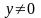 ,
4)
,
4)
 ,
если
,
если
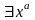 ,
5)
,
5)
 ,
6)
,
6)
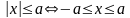 для
для
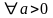 ,
7)
,
7)
 ,8)
,8)
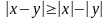 .
.
Определение
4.
Числовая
функция
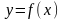 называется четной,
если
называется четной,
если
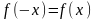 для всех
для всех
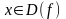 .
.
График четной функции симметричен относительно оси ординат.
Определение
5.
Числовая
функция
называется нечетной,
если
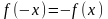 для всех
.
для всех
.
Определение
6. Функция
называется
периодической с периодом
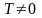 ,
если
,
если
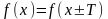 для любого
.
для любого
.
Определение
7.
Функция
называется ограниченной, если существует
такое число
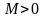 ,
что для всех
выполняется неравенство:
,
что для всех
выполняется неравенство:
 .
.
Определение
8.
Функция
называется возрастающей
(убывающей)
на множестве
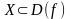 ,
если для любых
,
если для любых
 из неравенства
из неравенства
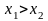 следует неравенство
следует неравенство
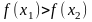 (
(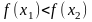 ).
).
Определение
9.
Функция
называется обратимой,
если разным значениям аргумента
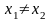 соответствуют
разные значения функции
соответствуют
разные значения функции
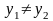 .
.
Определение
10. Основными
элементарными функциями являются:
постоянная
функция
(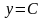 ),
степенная
(
),
степенная
(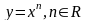 ),
показательная
(
),
показательная
(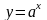 ),
логарифмическая
(
),
логарифмическая
( ),
тригонометрические
(
),
тригонометрические
(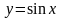 ,
,
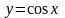 ,
,
 ,
,
 )
и обратные
тригонометрические (
)
и обратные
тригонометрические (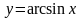 ,
,
 ,
,
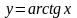 ,
,
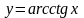 ).
).
22. Числовая последовательность и ее предел. Сходимость числовой последовательности.
Определение
1. Функция
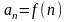 ,
областью определения которой является
множество натуральных чисел
,
областью определения которой является
множество натуральных чисел
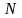 ,
называется функцией натурального
аргумента, или числовой
последовательностью.
,
называется функцией натурального
аргумента, или числовой
последовательностью.
Определение
2. Число
называется пределом
числовой последовательности
 ,
если для любого положительного сколь
угодно малого числа
,
если для любого положительного сколь
угодно малого числа
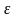 найдется такое натуральное число
,
что для всех
найдется такое натуральное число
,
что для всех
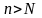 выполняется неравенство
выполняется неравенство
 .
.
Обозначение предела:
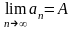
23. Предел функции в точке, предел функции в бесконечности. Бесконечно малые функции. Предел монотонных функций.
Определение
3.
Число
называется пределом функции
при
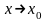 ,
если для любого положительного сколь
угодно малого числа
существует
,
если для любого положительного сколь
угодно малого числа
существует
 ,
такое что для всех
,
для которых
,
такое что для всех
,
для которых
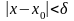 ,
выполняется неравенство
,
выполняется неравенство
 .
.
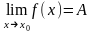 . Число
. Число
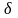 определяет некоторую
-окрестность
точки
определяет некоторую
-окрестность
точки
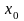 , т.е. интервал
, т.е. интервал
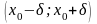 ,
содержащий точку
.
,
содержащий точку
.
4. Свойства пределов:
1.
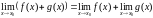 .
.
2.
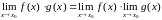 .
.
3.
Если
 ,
то
,
то
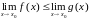 .
.
Лемма о пределе промежуточной функции (лемма о двух милиционерах):
Если
 и
и
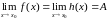 ,
то
,
то