3. Арифметические операции в двоичной системе счисления. Представление вещественных чисел в компьютере. Сложение и вычитание вещественных чисел в двоичной системе счисления.

Любое вещественное число N, представляемое в системе счисления с основанием p, можно представить в виде

N = + M · p^{+ k}, где M – мантисса, k – порядок числа (целое число)

234,47₁₀ = 0,23447 · 10³

1011,01₂ = 0,101101 · 10¹⁰⁰ , здесь мы учли, что 2₁₀ = 10₂ и 4₁₀ = 100₂

Это представление числа, называется представлением с плавающей точкой, где порядок определяет, на сколько необходимо осуществить сдвиг относительно запятой. Когда плавающая запятая размещена в мантиссе перед первой значащей цифрой, то такая форма записи — нормализованная, как в случаях, описанных выше.

Я не знаю, как это описать словами, поэтому рассмотрим пример из учебника:

A = - 100111010,00100110011001 * 2⁰ = - 0,10011101000100110011001 * 2⁹

B = + 11011,001011100001010001 * 2⁹ = + 0,11011001011100001010001 * 2⁵

Смещенный порядок числа А будет равен P*_A = P_A + N = 9 + 128 = 137₁₀ = 1000 1001₂

Смещенный порядок числа B будет равен P*_B = P_B + N = 5 + 128 = 133₁₀ = 1000 0101₂

Запишем числа в заданном формате:

A: 1.10001001. 10011101000100110011001;

B: 0.10000101. 11011001011100001010001;

Для выполнения операции сложения необходимо выровнять порядки чисел, т.е. принять порядок меньшего числа (B) равным порядку большего числа (A), уменьшив мантиссу меньшего путем сдвига вправо на число разрядов, равное разности порядков чисел P_A – P_B = 4:

B: 0.10001001. 000011011001011100001010001

Мантиссу отрицательного числа M_А представляем в дополнительном коде, положительного M_B в прямом. Тогда

M_A = 1.01100010111011001100110 – в обратном

M_A = 1.01100010111011001100111 – в дополнительном

M_A = 1.01100010111011001100111

+

M_B = 0.00001101100101110000101

M_A + M_B = 1.01110000100000111101100

Результат отрицательный в знаковом разряде 1, мантисса нормализованная. Запишем результат с учетом разрядной сетки заданного формата

A + B = 1.10001001.01110000100000111101100

т.к. Результат отрицательный,то мантисса записана в доп.коде, переведем доп.код в прямой(вычтем 1 и инвертируем цифры)

M_A + M_B = 1.01110000100000111101011 – в обратном

M_A + M_B = -0.10001111011111000010100 — в прямом

Проверка:

Рассчитаем порядок. 10001001 = 2⁷ + 2³ + 2⁰ = 128 + 8 + 1 = 137₁₀

Или с учетом смещения 138 - 128 = 9

Тогда, т.к. Мантисса имеет вид: -0.10001111011111000010100, то с учетом порядка имеем:

100011110.11111000010100(сдвинули точку на 9 позиций).

Значит целая часть результата:

2⁸ + 2⁴ +2³ +2² = 256 + 16 + 8+ 4 +2 = 286₁₀

Дробная часть результата:

2^-1+2^-2+2^-3+2^-4+2^-5 = 0, 96875 ≈ 0,97

Эти же числа А и B сложим в 10ой системе: -314,15 + 27,18 = -286,97

4. Основные логические операции: and, or, not, xor. Таблицы истинности для этих операций. Основные тождества булевой алгебры.

Как и любая другая, Булева алгебра использует переменные и операции над ними. В данном случае переменные и операции являются логическими переменными и логическими операциями. Переменные могут принимать только два значения - ИСТИНА (1) и ЛОЖЬ (0).

Базовые логические операции — конъюнкция (AND), дизъюнкция (OR) и инверсия (NOT), которые символично представляются знаками точки, плюса, надчеркивания:

A AND B = A ● B ;

A OR B = A + B ;

NOT A = ;

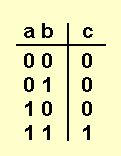
Результатом операции AND будет 1, тогда и только тогда когда оба операнда 1.

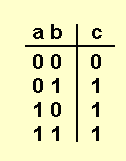
Результатом операции OR будет 0, тогда и только тогда когда оба операнда 0.

Унарная операция NOT инвертирует значение операнда.

При отсутствии скобок, существует приоритет операции AND над OR.

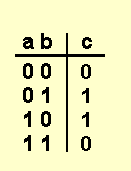
Операция XOR — сумма по ислючительное ИЛИ, дает 1 тогда и только тогда, когда один операнд 1.

Далее приведены таблицы истинности для этих операций.

AND OR NOT XOR

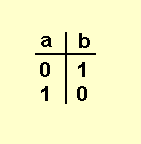
Далее приведены основные тождества Булевой Алгебры:

Постулаты
A●B = B●A	A+B=B+A	Коммутативные законы
A●(B+C)=A●B + A●C	A+(B●C)=(A+B)●(A+C)	Дистрибутивные законы
1●A=A	0+A=A
A● =0	A+ =1
Производные тождества
0●A=0	1+A=1
A●A=A	A+A=A
A●(B●C)=(A●B)●C	A+(B+C)=(A+B)+C	Ассоциативные законы
= +	= ●	Формулы де Моргана

5. Графические обозначения основных логических операций: AND, OR, NOT. Схема двоичного сумматора и ее анализ.

AND OR NOT XOR

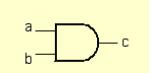
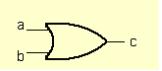
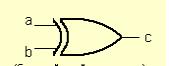
Схема двоичного сумматора и ее анализ.

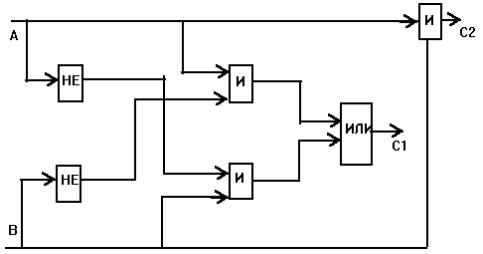
AB + ( B+ A)