Билет № 6: Системы счисления основные понятия.

Система счисления - это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе:  ; ;   и т. д.

Различают два типа систем счисления:

• позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;

• непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.

Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является десятичная система, используемая повседневно.

Любое целое число в позиционной системе можно записать в форме многочлена:

где S - основание системы счисления;

 - цифры числа, записанного в данной системе счисления;

n - количество разрядов числа.

Пример. Число   запишется в форме многочлена следующим образом:

 

Билет № 8: Алгоритм перевода целых чисел методом деления.

Метод поэтапного деления на основание с.с. заключается в последовательном выполнении действий:

1. Исходное число делим на основание с.с. с остатком в десятичной с.с.

2. Если часное от деления не равно 0, выпоняем п.1.

3. Полученные остатки записываем последовательно от последнего к первому.

4. Полученная запись - искомое двоичное число.

 

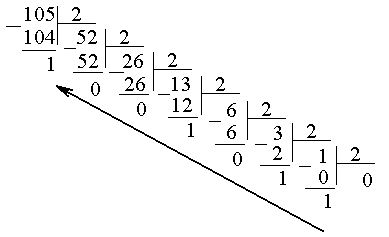
Например: переведем число 105 в двоичную с.с. методом поэтапного деления на основание с.с.

105₁₀ = 1101001₂

Методом поэтапного деления можно перевести целое десятичное число в любую позиционную систему счисления.

Билет №9 Алгоритм перевода правильной дроби методом деления. Пример

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

.116 • 2 = 0.232

.232 • 2 = 0.464

.464 • 2 = 0.928

.928 • 2 = 1.856

.856 • 2 = 1.712

.712 • 2 = 1.424

.424 • 2 = 0.848

.848 • 2 = 1.696

.696 • 2 = 1.392

.392 • 2 = 0.784

и т. д.

Получим: 206,11610=11001110,00011101102

Билет № 10: Алгоритм перевода чисел методом «взвешивания». Билет № 11: Алгоритм перевода чисел из 2-чн методом «замены».

1. Для того чтобы перевести число из двоичной системы в восьмерич­ную, необходимо выполнить следующие действия. Двигаясь от запятой влево и вправо, разбить двоичное число на группы по три разряда, допол­няя при необходимости нулями крайние левую и правую группы. Затем триаду заменить соответствующей восьмеричной цифрой.

Пример. Перевести число 10011001111,0101 из двоичной системы в восьмеричную.

Решение:

Триады	010	011	001	111	,	010	100
Восьмеричные цифры	2	3	1	7	,	2	4

Ответ: 2317,24₈.

2.Для перевода числа из восьмеричной системы в двоичную достаточно заменить каждую цифру этого числа соответствующим трёхразрядным двоичным числом (триадой), при этом отбрасывают незначащие нули в старших и младших (после запятой) разрядах.

Пример. Перевести число 204,4 из восьмеричной системы в двоичную.

Решение. 

Восьмеричные цифры	2	0	4	,	4
Триады	010	000	100	,	100

Ответ: 10000100,1₂.

3.  Для перевода числа из шестнадцатеричной системы в двоичную достаточно заменить каждую цифру этого числа соответствующим четырёхразрядным двоичным числом (тетрадой), при этом отбрасывают незначащие нули в старших и младших (после запятой) разрядах.

Пример. Перевести число 6СЗ,А из шестнадцатеричной системы в двоичную.

Решение:

Шестнадцатеричные цифры	6	C	3	,	A
Тетрады	0110	1100	0011	,	1010

Ответ: 11011000011,101₂.