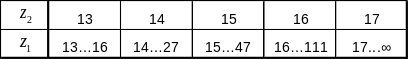- •Лекция № 1 механические передачи.
- •Основные термины и определения.
- •1.2. Требования к механическим передачам и их классификация.
- •1.3. Передаточное отношение.
- •1.4. Мощность.
- •1.5. Коэффициент полезного действия.
- •Лекция № 2
- •2.1. Кинематические характеристики передач.
- •2.2. Динамические исследования передач.
- •2.3. Силовой расчет передач.
- •2.4. Основные критерии работоспособности расчета элементов приборного устройства.
- •Лекция № 3. Механические механизмы.
- •3.1. Кулачковые механизмы.
- •3.2. Рычажные механизмы.
- •3.2.1. Синусный и тангенсный механизмы.
- •3.2.2. Поводковый механизм.
- •3.2.3. Кривошипно – шатунный механизм.
- •Лекция № 4.
- •4.1. Кулисный механизм.
- •Мальтийский крест.
- •Храповые механизмы.
- •2.3. Механизмы с гибкими звеньями.
- •Лекция № 5. Фрикционные передачи.
- •2.1. Классификация фрикционных передач.
- •2.2. Расчет фрикционных передач.
- •Лекция № 6.
- •6.1. Кинематические и силовые соотношения фрикционных передач.
- •6.2. Определение силы прижатия.
- •6.3. Материалы.
- •6.4. Достоинства, недостатки и рекомендации.
- •Лекция № 7. Зубчатые передачи.
- •7.1. Классификация зубчатых передач.
- •7.2. Основные понятия.
- •7.3. Основные параметры.
- •7.4. Основная теорема зацепления.
- •7.5. Скольжение профилей
- •7.6. Общие требования к профилям зубьев.
- •Лекция № 8.
- •8.1. Цилиндрическая зубчатая эвольвентная передача.
- •8.2. Выбор участка эвольвенты для профиля зуба колеса.
- •В соответствии с обозначениями рис. 8.3 справедливы следующие силовые соотношения. Окружная сила для каждого их профилей колеса может быть определена по формуле:
- •9.2. Виды зубчатых колёс в зависимости от толщины зуба по делительной окружности
- •9.3. Основные параметры зацепления двух нулевых колес эвольвентного профиля и передачи.
- •Лекция № 10.
- •10.1. Реечное зацепление.
- •10.2. Основные свойства эвольвентного зацепления.
- •10.3. Методы нарезания зубьев колес.
- •10.4. Интерференция в эвольвентном зацеплении
- •Лекция № 11.
- •11.1. Определение минимального числа зубьев колеса из условия предупреждения интерференции.
- •11.2. Коррегирование эвольвентного зацепления.
- •11.3. Эвольвентные зубчатые передачи с внутренним зацеплением зубьев.
- •Лекция № 12. Расчёты зубчатых колёс на прочность.
- •12.1. Виды повреждений зубьев
- •12.3. Расчёт зубчатых передач на изгибную прочность зубьев.
- •Лекция № 13.
- •13.1. Расчёт цилиндрических эвольвентных зубчатых колёс на контактную прочность.
- •Лекция № 14.
- •14.1. Основные характеристики и параметры приборных электродвигателей.
- •14.2. Многоступенчатые зубчатые передачи. Основные понятия.
- •14.3. Классификация многоступенчатых зубчатых передач.
- •Лекция № 15. Косозубые цилиндрические колеса.
- •15.1. Геометрические параметры.
- •15.2. Коэффициент торцевого перекрытия.
- •15.3. Расчёт косозубых колёс на прочность.
- •Лекция № 16. Конические передачи.
- •16.1. Геометрические и кинематические соотношения
- •16.2. Особенности расчёта на прочность конических прямозубых передач.
- •16.3. Особенности конических передач.
- •Основная литература.
10.4. Интерференция в эвольвентном зацеплении
Контакт эвольвентных профилей в зацеплении теоретически возможен в пределах линии зацепления - отрезка (рис. 10.1, а).
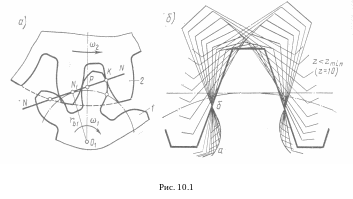
В реальной передаче вхождение зубьев
в зацепление перед точкой
![]() и выход из зацепления после точки
и выход из зацепления после точки
![]() приводят к интерференции зубьев, то
есть их перекрытию. В
приводят к интерференции зубьев, то
есть их перекрытию. В
В этом случае в зубчатой передаче
происходит заклинивание. При нарезании
колёс методом обкатки (фрезой, гребёнками,
долбяком) интерференция является
причиной подрезания ножки зубьев колеса
в месте перекрытия эвольвент. Это
приводит к утончению ножки и укорочению
профиля. Основной причиной появления
интерференции является уменьшение
числа зубьев шестерни ниже предельного
значения
![]() .
Уменьшение числа зубьев шестерни
применяется, исходя из конструктивных
соображений, для увеличения передаточного
отношения при сохранении заданного
межосевого расстояния.
.
Уменьшение числа зубьев шестерни
применяется, исходя из конструктивных
соображений, для увеличения передаточного
отношения при сохранении заданного
межосевого расстояния.
Лекция № 11.
11.1. Определение минимального числа зубьев колеса из условия предупреждения интерференции.
Для прямозубых колёс, нарезаемых
инструментом реечного типа (гребёнки,
червячные фрезы, долбяки), с уменьшением
числа зубьев шестерни и суммарного
числа зубьев в передаче уменьшается
коэффициент перекрытия
.
Из этого следует, что нарушается плавность
работы передачи, возрастает скорость
скольжения профилей и снижается КПД
передачи. В колёсах с числом зубьев
меньше 17 при нарезании зубьев колеса
происходит подрезание ножки зуба. При
этом, во-первых, уменьшается рабочая
высота зуба, во вторых, уменьшается
прочность зуба, в- третьих, уменьшается
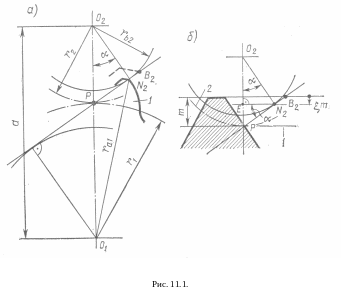
длина зацепления. На рис. 11.1 а представлено
предельное положение зубьев перед
появлением интерференции, когда вершина
зуба ведущего колеса 1 проходит через
конечную точку
линии зацепления. Этому положению
соответствует минимально допустимое
число зубьев малого колеса
,
а также равенство начальной и делительной
окружностей
![]() (
(![]() - радиусы делительных окружностей,
- радиусы делительных окружностей,
![]() - радиус окружности впадин ведомого
колеса 2).
- радиус окружности впадин ведомого
колеса 2).
![]()
При смещении точки контакта по линии
в точке
эвольвента будет полностью использована
для передачи движения. При уменьшении
числа зубьев колеса 2 вершина зуба колеса
1 перейдёт в точку
![]() .
При этом эвольвента 1 «наложится» на
эвольвенту 2, и произойдёт заклинивание.
Если большее колесо является режущим
инструментом, то произойдёт подрезание
зуба малого колеса (шестерней).
.
При этом эвольвента 1 «наложится» на
эвольвенту 2, и произойдёт заклинивание.
Если большее колесо является режущим
инструментом, то произойдёт подрезание
зуба малого колеса (шестерней).
Найдём условие, при котором возможно правильное зацепление без заклинивания и подрезания.
Рассмотрим
![]() :
:
![]() .
.
Произведём замены:
![]() ;
;
![]() ;
;
![]() .
.
В этом случае получаем:
![]() ;
;
![]() .
.
После сокращения и упрощений получим:
![]() .
.
Рассмотрим решение этого уравнения для двух частных случаев:
Пусть передаточное отношение в зацеплении равно:
а)
![]() ,
тогда
,
тогда
![]() :
:
![]() ;
;
б)
![]() ,
тогда
,
тогда![]() ,
т. е. колесо 1 представляет собой рейку,
а колесо
,
т. е. колесо 1 представляет собой рейку,
а колесо
![]() .
.
Из полученного выражения следует, что при условии равенства числа зубьев первого колеса число зубьев второго колеса .
Задавая для
![]() промежуточные значения от
до
,
можно найти минимальные значения чисел
зубьев шестерни (малого колеса),
приведённые в таблице.
промежуточные значения от
до
,
можно найти минимальные значения чисел
зубьев шестерни (малого колеса),
приведённые в таблице.
Таблица 1.