Вычисление предела последовательности.

Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся. Для сходящихся последовательностей справедливы теоремы, вытекающие из определения предела:

1.

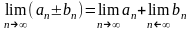
2.

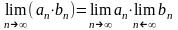
3.

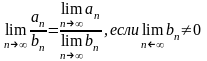
Пример 1. Найти предел:

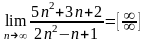
Как показывает решение задачи, подстановка предельного значения приводит к неопределенности 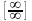. Часто встречаются неопределенности вида 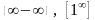. Нахождение предела последовательности в этих случаях называют раскрытием неопределенности. Для раскрытия неопределенности приходится, прежде чем перейти к пределу, проводить преобразования данного выражения.

Решение примера 1: Поделим числитель и знаменатель на наивысшую степень n, в данном случае на n :

.

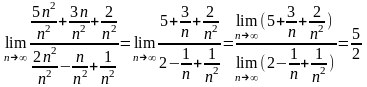Т.к. (см. пр.3 Л.р.№3).

Пример 2. Найти предел:

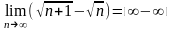
Решение: Умножим и разделим выражение, стоящее под знаком предела на выражение сопряженное ему:

.

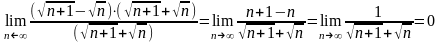Пример 3.Найти предел:

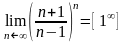
Решение: Воспользуемся 2-м замечательным пределом:

= .

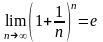
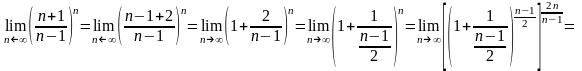
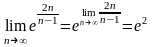Предел функции.

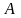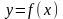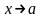Опр.1.Число называется пределом функции при , если для любой окрестности 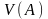числа существует такая проколотая окрестность 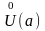числа a, что для всех ,

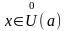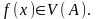
Это определение по Коши. Число может быть как конечным, так и бесконечным. В частности, если числа и а конечны, получаем следующее определение (на языке “ - ”).

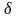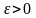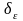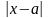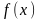Опр.2. Число называется пределом функции при , если для всякого существует такое число >0, что для всех х, удовлетворяющих неравенству 0< < и входящих в область определения функции , справедливо неравенство:

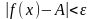(1)

и обозначается

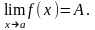
Если а = +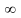 , то получаем следующее определение.

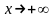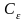Опр.3.Число называется пределом функции при , если для всякого существует такое число >0, что для всех х, удовлетворяющих неравенству 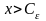и входящих в область определения функции , справедливо (1) и обозначается:

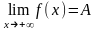(определение “ -C”).

Определение предела функции по Гейне: Число А называется пределом функции y=f(x) при (в точке a), если для любой сходящейся к числу а последовательности 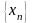значений х, входящих в область определения функции и отличных от a, соответствующая последовательность 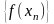этой функции сходится к числу А.

Пример 1. Пользуясь определением предела по Гейне, доказать, что

.

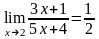Решение: Рассмотрим любую последовательность , удовлетворяющую двум условиям:

1)

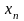
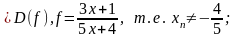
2) .

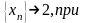
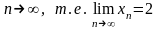Этой последовательности соответствует последовательность значений функции:

…

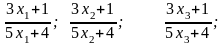Тогда на основании свойств сходящихся последовательностей (каких?) будем иметь

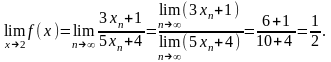
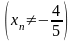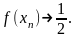Т.о. независимо от выбора последовательности , сходящейся к числу 2 , соответствующая последовательность значений функции А это на основании определения предела функции по Гейне значит, что

Замечание 1: Определением предела по Гейне удобно пользоваться тогда, когда доказывается, что функция f(x) не имеет предела. Для этого достаточно показать, что существует две последовательности 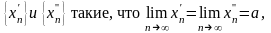но соответствующие последовательности 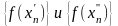имеют неравные пределы.

Пример 2: Доказать, что 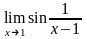не существует.