44.Теорема Ролля

Если вещественная функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю

Теорема Лагранжа (обобщение теоремы Ролля)

y = f (x) – непрерывна при х  [a; b] и

дифференцируема при х  (a; b) 

 c  (a; b):

45.Теорема Коши

Пусть даны две функции и такие, что:

1. и определены и непрерывны на отрезке ;

2. производные 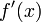и конечны на интервале ;

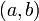3. производные и не обращаются в нуль одновременно на интервале

4. ;

тогда

, где

(Если убрать условие 4, то необходимо усилить условие 3: g'(x) не должна обращаться в ноль нигде в интервале (a,b).)

Доказательство

Для доказательства введём функцию

Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а равна как раз необходимому числу.

Лагра́нжа о среднем значении

утверждает, что если функция f непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b), то найдётся такая точка , что

.

Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

46.Исследование функции

Пусть дана функция . Для её исследования нужно:

1). Найти её область определения . Если это не слишком сложно, то полезно найти также область значений . (Однако, во многих случаях, вопрос нахождения откладывается до нахождения экстремумов функции.)

2). Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной (быть может, после сдвига влево или вправо по оси ), не является ли она периодической.

3). Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определения , если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.

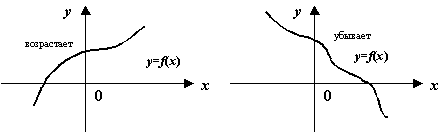
Возрастающая, убывающая функция

Напомним, что функция называется возрастающей на интервале , если для любых двух точек из неравенства следует, что ; убывающей на интервале , если из неравенства следует, что ;

47=48=49.Экстремум функции

Экстре́мум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Достаточные условия экстремума

Пусть задана z =z (x,y), (x,y) D, которая имеет частные производные второго порядка в некоторой окрестности точки M₀(x₀,y₀) D. Причем M₀ - стационарная точка (т. е. необходимые условия (1.41) выполнены). Вычислим:

Если:

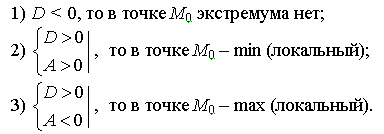
Доказательство теоремы использует темы (формула Тейлора функции нескольких переменных и теория квадратичных форм), которые в этом пособии не рассматриваются.

Необходимые условия экстремума

Пусть задана функция z =z (x,y), (x,y) D. Точка M₀(x₀;y₀ D - точка локального экстремума.

Если в этой точке существуют z'_x и z'_y, то

Геометрическое доказательство "очевидно". Если в точке C₀ на (рис.1.4) провести касательную плоскость, то она "естественно" пройдет горизонтально, т. е. под углом 0° к оси Ох и к оси Оу.

Тогда в соответствии с геометрическим смыслом частных производных (рис.1.3):

что и требовалось доказать.

50.=33.

51.=46 Выпуклость и вогнутость

График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).

52=46