- •25.Множества чисел
- •26.Функция
- •27.Числовые последовательности
- •28.Предел функции непрерывного аргумента
- •29. Свойства бесконечно малых функций
- •31.Теорема о двух милиционерах
- •33. Свойства пределов функции
- •Первый замечательный предел
- •Второй замечательный предел
- •34.Непрерывность функции
- •Односторонний предел по Гейне
- •Односторонний предел по Коши
- •35.Свойства функций непрерывных на промежутке
- •36. Теорема о непрерывности дифференцируемой функции
- •37.Производная функции в точке
- •Производная показательной функции
- •Производная логарифмической функции
- •39. Производная сложной функции
- •40. Производная обратной функции
- •41.Производная функций заданных неявно
- •42.Дифференциал функции
- •Свойства дифференциала.
- •43. Производные высших порядков
- •44.Теорема Ролля
- •Теорема Лагранжа (обобщение теоремы Ролля)
- •45.Теорема Коши
- •Доказательство
- •46.Исследование функции
- •Необходимое условие точки перегиба
- •Достаточное условие точки перегиба
- •54.Исследование схема Общая схема исследования функции
Производная логарифмической функции
Производная функции y = ln x существует и выражается формулой
![]() (15)
(15)
В случае сложной логарифмической функции y = ln u, где u – дифференцируемая функция аргумента x, формула (15) примет вид
![]() (16)
(16)
Пользуясь формулой (16), найдём производную логарифмической функции с произвольным положительным основанием a. Пусть
![]()
На основании свойств логарифмов имеем
![]()
Так как
![]()
- постоянный множитель, то
![]()
или
![]()
38.
Производные элементарных функций:
Функция |
Производная |
f(x) = C, C ∈ R |
0 (да-да, ноль!) |
f(x) = xn |
n · xn − 1 |
f(x) = sin x |
cos x |
f(x) = cos x |
− sin x |
f(x) = tg x |
1/cos2 x |
f(x) = ctg x |
− 1/sin2 x |
f(x) = ln x |
1/x |
f(x) = loga x |
1/(x · ln a) |
f(x) = ex |
ex |
![]()
![]()
![]()
39. Производная сложной функции
Пусть
функция f:
[a,
b]
→ [c,
d],
а функция g:[a1,
b1]
→ [c1,
d1],
причём [a1,
b1]
![]() [c,
d].
Если функция f
дифференцируема в точке х0
[a,
b],
а функция g
дифференцируема в точке y0
= f
(x0)
[a1,b1],
то сложная функция F(x)
= g(
f
( x ))
имеет в точке х0
производную, равную
[c,
d].
Если функция f
дифференцируема в точке х0
[a,
b],
а функция g
дифференцируема в точке y0
= f
(x0)
[a1,b1],
то сложная функция F(x)
= g(
f
( x ))
имеет в точке х0
производную, равную
g ' ( f ( x0 ) )·f ' ( x0 ).
Показательно-степенная функция
Показательно-степенной функцией называется функция вида y = uv, где u=u(x), v=v(x).
Логарифмическое дифференцирование применяется для нахождения производной от показательно-степенной функции.
40. Производная обратной функции
Теорема. Пусть функция х = f(y) монотонна и дифференцируема в некотором интервале (a, b) и имеет в точке у этого интервала производную f'(y), не равную нулю. Тогда в соответствующей точке х обратная функция у = f--1(x) имеет производную [f--1(x)]', причем
![]() или
или
![]()
Производные обратных тригонометрических функций
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
41.Производная функций заданных неявно
Если функция y=y(x) задана неявно уравнением F(x,y)=0 , F(x,y) — дифференцируемая функция и F 'y( x, y) не равен 0, то производная y'(x) вычисляется по формуле y'(t) = - F'x(x, y) / F'y(x, y).
Производная функций заданных параметрически
формула
производной параметрически заданной
функции
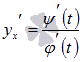
42.Дифференциал функции
Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f’(x)dx.
Свойства дифференциала.
Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u ± v) = (u ± v)’dx = u’dx ± v’dx = du ± dv
2) d(uv) = (uv)’dx = (u’v + v’u)dx = vdu + udv
3) d(Cu) = Cdu
4)
![]()
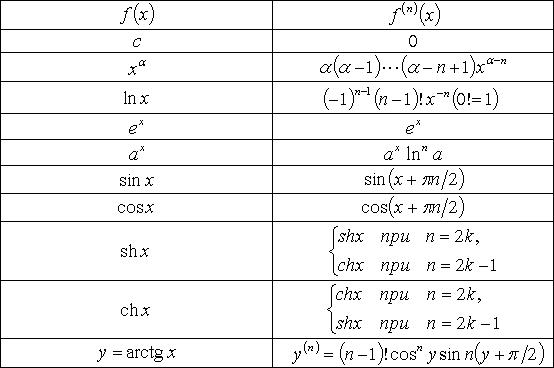
43. Производные высших порядков
Если
функция
![]() дифференцируема
при всех
дифференцируема
при всех
![]() ,
то мы можем рассмотреть функцию
,
то мы можем рассмотреть функцию
![]() ,
сопоставляющую каждой точке
,
сопоставляющую каждой точке
![]() значение
производной
значение
производной
![]() .
Эта функция
.
Эта функция
![]() называется
производной функции
называется
производной функции
![]() ,
или первой
производной
от
.
(Иногда саму исходную функцию
называют
нулевой
производной и
обозначают тогда
,
или первой
производной
от
.
(Иногда саму исходную функцию
называют
нулевой
производной и
обозначают тогда
![]() .)
Функция
.)
Функция
![]() ,
в свою очередь, может иметь производную
во всех (или некоторых) точках
интервала
,
в свою очередь, может иметь производную
во всех (или некоторых) точках
интервала
![]() ,
которую мы обозначим
,
которую мы обозначим
![]() и
назовём второй
производной
функции
.
Если предположить, что вторая производная
и
назовём второй
производной
функции
.
Если предположить, что вторая производная
![]() существует
во всех точках
,
то она может также иметь производную
существует
во всех точках
,
то она может также иметь производную
![]() ,
называемую третьей
производной
функции
,
и т. д. Вообще,
,
называемую третьей
производной
функции
,
и т. д. Вообще,
![]() -й
производной
функции
называется
производная от предыдущей,
-й
производной
функции
называется
производная от предыдущей,
![]() -й
производной
-й
производной
![]() :
:
![]()