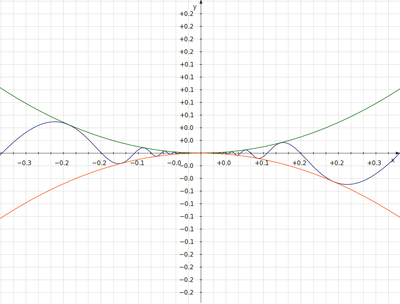
31.Теорема о двух милиционерах

Если функция y = f(x) такая, что для всех x в некоторой окрестности точки a, причем функции φ(x) и ψ(x) имеют одинаковый предел при , то существует предел функции y = f(x) при , равный этому же значению, то есть

32. Вторая теорема Вейерштрасса

  Непрерывная на отрезке [a, b] функция ограничена и достигает на этом отрезке своей верхней и своей нижней грани    Доказательство. Пусть f (x) C_{[a, b]} (функция принадлежит классу непрерывных функций на отрезке [a, b]) и пусть . Согласно определению верхней грани функции, для каждого n существует такая точка х_n [а, b], что

,

Из последовательности x_n [а, b] можно выделить сходящуюся к некоторому значению х₀ подпоследовательность:

.

В силу непрерывности функции имеем далее

.

В то же время

.

И в пределе f (x₀) M. Но f (x₀) не может быть больше верхней границы М и, следовательно, f (x₀) = М. Что и требовалось доказать

33. Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

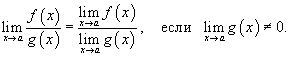
Первый замечательный предел

Доказательство

Рассмотрим односторонние пределы и и докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

(1)

(где S_sectOKA — площадь сектора OKA)

(из : | LA | = tgx)

Подставляя в (1), получим:

Так как при :

Умножаем на sinx:

Перейдём к пределу:

Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Второй замечательный предел

или

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что

Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где  — это целая часть x.

Отсюда следует: , поэтому

.

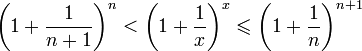Если , то . Поэтому, согласно пределу , имеем:

.

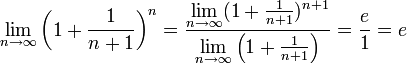
По признаку (о пределе промежуточной функции) существования пределов .

Раскрытие неопределенностей

Для раскрытия неопределённостей типа используется следующий алгоритм:

1. Выявление старшей степени переменной;

2. Деление на эту переменную как числителя, так и знаменателя.

Для раскрытия неопределённостей типа существует следующий алгоритм:

1. Разложение на множители числителя и знаменателя;

2. Сокращение дроби.

Правило Лопиталя

. Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или . Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

(1)