Способы определения

Число e может быть определено несколькими способами.

• Через предел:

 (второй замечательный предел).

• Как сумма ряда:

 или  .

• Как единственное число a, для которого выполняется

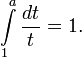
• Как единственное положительное число a, для которого верно

Свойства

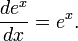• Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения   является функция  , где c — произвольная константа.

• Число e иррационально и даже трансцендентно. Его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.

• Число e является вычислимым (а значит, и арифметическим) числом.

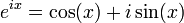• , см. формула Эйлера, в частности

  • 

• Ещё одна формула, связывающая числа е и π, т. н. «интеграл Пуассона» или «интеграл Гаусса»

• Для любого комплексного числа z верны следующие равенства:

• Представление Каталана:

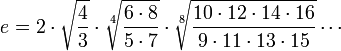
• Мера иррациональности (англ.) числа e равна 2 (что есть наименьшее возможное значение для иррациональных чисел).

Второй замечательный предел

Второй замечательный предел имеет вид:   или в другой записи 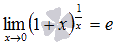  В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность  . Разберем несколько примеров нахождения предела по второму замечательному пределу с подробным оприсанием решения.  Пример. Вычислить предел  Решение. Подставляем бесконечность: Пришли к неопределенности единица в степени бесконечность. Смотрим в таблицу неопределенностей для определения метода решения и останавливаемся на применении второго замечательного предела. Сделаем замену переменных. Пусть Если  , то  Исходный предел после замены примет вид: Ответ:  Пример. Вычислить предел  Решение. Подставляем бесконечность: Пришли к неопределенности единица в степени бесконечность, которая указывает на применение второго замечательного предела. Выделим целую часть в основании показательно степенной функции: Тогда предел запишется в виде: Сделаем замену переменных. Пусть Если  , то  Исходный предел после замены примет вид:   В преобразованиях были использованы свойства степени и свойства пределов. Ответ: 

10)

Предел функции по Коши

Значение   называется пределом (предельным значением) функции   в точке  , если для любого наперёд взятого положительного числа ε найдётся отвечающее ему положительное число   такое, что для всех аргументов  , удовлетворяющих условию  , выполняется неравенство  .^[1]

Окрестностное определение по Коши

Значение   называется пределом (предельным значением) функции   в точке  , если для любой окрестности   точки   существует выколотая окрестность   точки   такая, что образ этой окрестности   лежит в  . Фундаментальное обоснование данного определения предела можно найти в статье Предел вдоль фильтра.

Геометрическая интерпретация предела функции.

   Обратимся к рисунку 1, на котором представлен фрагмент графика функции   .

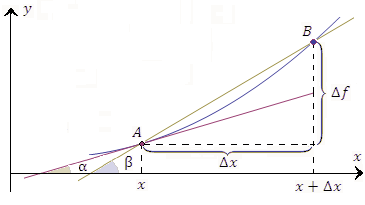  Рис. 1. Секущая  AB  образует угол  β  с положительным направлением оси  0x. Касательная к графику функции проведена в точке  A.

      Угловой коэффициент секущей  AB  равен средней скорости изменения функции     на промежутке  [x, x + ∆x]:

(5)

Предельным положением секущей  AB  при перемещении точки  B  к точке  A  по дуге кривой     является касательная к графику в точке  A. Поэтому угловой коэффициент касательной равен пределу углового коэффициента секущей при  ∆x → 0:

(6)

  Рис. 2. Касательная является предельным положением секущей  AB  при перемещении точки  B  к точке  A.

      Таким образом, производная     в точке  x  равна тангенсу угла, образованного касательной к графику функции     в этой точке с положительным направлением оси  0x.

11)

Пусть переменная  x  стремится к  a, оставаясь больше  a, и при этом   . Тогда число  A  называют правосторонним пределом (или пределом справа) функции     и обозначают любым из символических выражений Понятие левостороннего предела (или предела слева) вводится аналогичным образом. В этом случае     при  x → a  со стороны меньших значений: Для существования обычного (двустороннего) предела функции     в точке  a  необходимо и достаточно равенство между собой односторонних пределов:   Например, в точке  x = 3  односторонние пределы функции отличаются друг от друга:   Поэтому в рассматриваемой точке предел функции     не существует.

12) Первым замечательным пределом именуют  . Известны также и следствия из первого замечательного предела:

       Все приведенные выше формулы получаются из основной:  . Примечательность последней формулы состоит в том, что вместо х можно подставлять любое выражение, лишь бы это выражение стремилось к нулю. Например, так как при  , то  . Собственно говоря, на этом и основаны примеры на первый замечательный предел. Суть решения таких заданий проста: формально подогнать условие под вид первого замечательного предела, после чего использовать формулу  . Допустим, нужно найти  . Простой подстановкой   проблему не решить, потому как  , т.е. тут мы имеем дело с неопределенностью вида  . Если такая неопределенность встречается вкупе с тригонометрическими выражениями, то для стандартных типовых расчетов это почти стопроцентная гарантия первого замечательного предела. Подгоним данную задачу под вид упомянутого предела, учитывая  :

       Осуществим следующее преобразование: в числителе домножим на 7х и разделим на 7х. этим мы не изменяем значение числителя. Аналогичную операцию проделаем в знаменателе:

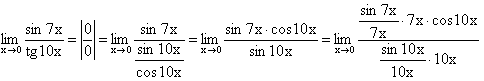
       Что нам это даст? Так как при   имеем  , то можно применить первый замечательный предел:  . Учитывая это, получим:

       Сокращая х и вспомнив, что  , получим:  . Приведем ещё несколько примеров решения задач на первый замечательный предел:

 

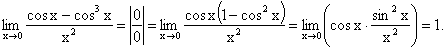
13) Классификация бесконечно малых функций

Во многих случаях представляет интерес сравнение бесконечно малых между собой по характеру их приближения к нулю. Рассмотрим две бесконечно малые (x) и (x) при xx0 и предположим, что (x) не обращается в ноль в некоторой проколотой окрестности точки x0. Будем сравнивать эти бесконечно малые, изучая поведение их отношения при xx0.

Дадим следующие определения.

Если  , то говорят, что (x) и (x) бесконечно малые одного порядка при xx0.

Если  , то говорят, что (x) бесконечно малая более высокого порядка по сравнению с (x) при xx0, и пишут  , xx0.

Если (x) и k(x) – бесконечно малые одного порядка (k>0), то говорят, что (x) величина k-го порядка относительно бесконечно малой (x) при xx0 и пишут  , xx0.

Если  , то говорят, что (x) и (x) эквивалентные бесконечно малые при xx0 и пишут  , xx0.

Замечание. Та же терминология применяется и при сравнении функций, не являющихся бесконечно малыми при xx0. В этом случае добавляется ещё одно определение.

Если существует число C > 0 такое, что в некоторой проколотой окрестности точки x0 справедливо неравенство  , то говорят, что функция (x) ограничена относительно функции (x) при xx0, и пишут  , xx0.

Примеры. 1. Привести примеры на каждое из определений.

2. Доказать, что   при x0.

3. Вычислить:  .

4. Доказать, что   при x0.

Логарифм по основанию e (e - трансцендентное число, приближенно равное 2,718281828...) называется натуральным логарифмом. Натуральный логарифм числа x обозначается ln x. Натуральные логарифмы широко используются в математике, физике и инженерных расчетах.

14) Непрерывная функция — функция без «скачков», то есть такая у которой малые изменения аргумента приводят к малым изменениям значения отображения. График непрерывной функции можно начертить «не отрывая карандаш от бумаги».

Непрерывная функция вообще говоря, — синоним понятия непрерывное отображение, тем не менее, чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающих вещественные значения.