
- •4 Числовые ряды. Основные определения.
- •Если ряд (2) сходится, то ряд (1) также сходится;
- •Если ряд (1) расходится, то ряд (2) расходится.
- •6 Некоторые очевидные свойства числовых рядов:
- •1)Теорема 1. На сходимость ряда не влияет отбрасывание конечного числа его членов.
- •12. Знакопеременные ряды. Абсолютная и условная сходимость.
- •13 Теорема Лейбница:
- •14. Знакочередующиеся ряды. Теорема Лейбница.
- •15. Функциональные ряды, область сходимости. Равномерная сходимость. Признак Вейерштрассе.
- •16. Основные свойства равномерно сходящихся функциональных рядов.
- •17. Основные свойства равномерно сходящихся функциональных рядов.
- •18. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости.
- •19. Радиус сходимости.
- •20.Разложение нек-х ф-й в ряд Маклорена:
- •21. Ряд Тейлора. Достаточное условие разложимости функции в степенной ряд. Ряд Тейлора.
- •28.Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события, непосредственный подсчет вероятности. Примеры.
- •29.Зависимые и независимые события. Произведение событий. Понятие условной вер-ти. Теорема умножения вер-тей с док-вом. Пример.
- •30.Формулы полной вер-ти и Байеса с док-вом. Примеры.
- •31 Повторение опытов
- •Функция и распределения случайной величины, её определение, свойства и график.
- •34 Непрерывная случайная величина (нсв). Вероятность отдельного взятого значения нсв. Математическое ожидание и дисперсия нсв. Функция распределения нсв.
- •38 То́чечная оце́нка в математической статистике — это число, вычисляемое на основе наблюдений, предположительно близкое к оцениваемому параметру.
- •40 Проверка статических гиротез
34 Непрерывная случайная величина (нсв). Вероятность отдельного взятого значения нсв. Математическое ожидание и дисперсия нсв. Функция распределения нсв.
Сл\в Х наз-ся непрерывной, если её Функция Распределения непрерывна в любой точке и дифференцируемая во всюду, кроме отдельных точек (точки излома).
Мат\ожиданием дискретной сл\в называется сумма произведений всех возможных значений сл\в на их вероятности.
![]() Мат\о
существует, если ряд, стоящий в правой
части равенства, сходится абсолютно.
С точки зрения вер-ти можно сказать,
что м\о приближенно = среднему
арифметическому наблюдаемых значений
сл\в.
Мат\о
существует, если ряд, стоящий в правой
части равенства, сходится абсолютно.
С точки зрения вер-ти можно сказать,
что м\о приближенно = среднему
арифметическому наблюдаемых значений
сл\в.
Пусть НСВ Х задана ФР F(x). Допустим, что все возможные значения сл\в принадлежат отрезку [a,b].
Мат\ож-м НСВ
Х, возможные значения которой принадлежат
отрезку [a,b], наз-ся определенный интеграл
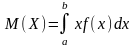 .
Если возможные значения сл\в рассм-ся
на всей числовой оси, то мат\о нах по
формуле:
.
Если возможные значения сл\в рассм-ся
на всей числовой оси, то мат\о нах по
формуле: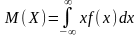 ,
при этом предпол-ся, что несобственный
интеграл сходится.
,
при этом предпол-ся, что несобственный
интеграл сходится.
Дисперсией
НСВ наз мат\ож квадрата ее отклонения.
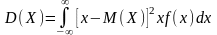 .
По аналогии с дисперсией, дискретной
сл\в, для практического вычисления
дисперсии используется формула:
.
По аналогии с дисперсией, дискретной
сл\в, для практического вычисления
дисперсии используется формула:
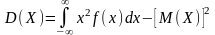 .
.
Функция распределения НСВ:
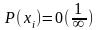 ,
в качестве способа задания НСВ
используется функция распределения
НСВ.
,
в качестве способа задания НСВ
используется функция распределения
НСВ.
ФРНСВ наз
вер-ть т\ч она примет значение меньшее
заданного.
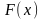 -обознач
ф-ии распр в-тей
-обознач
ф-ии распр в-тей
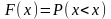
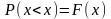
Основные свойства ф-ии распределения НСВ:
С1.
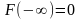
С2.
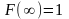
С3.
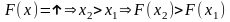
С4. Вер-ть
т\ч НСВ примет значение из интервала,
равна приращению ф-ии на этом интервале
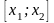
1)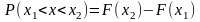
2)
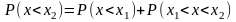
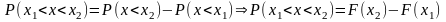
35 .Нормальный
закон распр также называется законом
Гаусса. НЗР занимает центральное место
в теории вероятностей. Это обусловлено
тем, что этот закон проявляется во всех
случаях, когда сл\в является результатом
действия большого числа различных
факторов. К НЗ приближаются все остальные
законы распределения. Можно легко
показать, что параметры 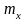 и
и
 ,
входящие в плотность распределения
являются соответственно мат\ожиданием
и средним квадратическим отклонением
сл\в Х.
,
входящие в плотность распределения
являются соответственно мат\ожиданием
и средним квадратическим отклонением
сл\в Х.
Найдем
функцию распределения F(x).
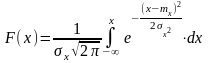
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.
Нормальная кривая обладает следующими свойствами:
1) Функция определена на всей числовой оси.
2) При всех х ф-я распр принимает только положительные значения.
3) Ось ОХ является горизонтальной асимптотой графика плотности вер-ти, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.
37 Выборка (выборочная совокупность) - часть объектов из генеральной совокупности, отобранных для изучения, с целью получения информации о всей генеральной совокупности.
Методы математической статистики позволяют оценить случайную ошибку изучаемых признаков выборки определенного объема. Также можно решить обратную задачу - определить объем выборки, удовлетворяющий заданным требованиям точности.
Кроме объема выборки, существенную роль играет способ формирования выборки. Не вдаваясь в детали, можно отметить, что выборка, которая сохраняет все свойства генеральной совокупности, называется репрезентативной выборкой. Свойство репрезентативности - необходимое условие для того, чтобы выводы, сделанные для выборочной совокупности, можно было распространить на генеральную совокупность.
