16. Основные свойства равномерно сходящихся функциональных рядов.
Непрерывность суммы.
В
области равномерной сходимости сумма
ряда
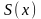есть ф-я непрерывная.
Следствие:
если функциональный ряд в некоторой
области Д сходится равномерно
то в этой области возможен предельный
переход:
.
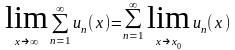В области равной сходимости функциональных рядов их можно почленно интегрировать.
.
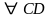
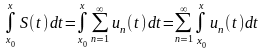Равномерносходящиеся ряды в области равной сходимости можно почленно диффериенцировать.
.
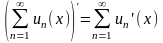17. Основные свойства равномерно сходящихся функциональных рядов.
Непрерывность суммы.
В области равномерной сходимости сумма ряда есть ф-я непрерывная.
Следствие: если функциональный ряд в некоторой области Д сходится равномерно то в этой области возможен предельный переход: .
В области равной сходимости функциональных рядов их можно почленно интегрировать.
.
Равномерносходящиеся ряды в области равной сходимости можно почленно диффериенцировать.
.
18. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости.
Степенным
рядом называется функциональный ряд
вида
,
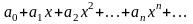где
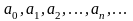- постоянные числа, называемые
коэффициентами ряда.
Теорема Абеля.
Если
степенной ряд сходится при некотором
значении
,
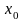не равном нулю, то он абсолютно сходится
при всяком х, для которого
.
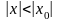Если
ряд расходится при некотором значении
,
то он расходится при всяком х, для
которого
.
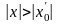Доказательство:
Так как по предположению числовой ряд
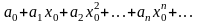сходится, то его общий член
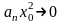при
,
а это значит, что существует такое
положительное число М, что все члены
ряда по абсолютной величине меньше М.
Перепишем ряд в виде
и
рассмотрим ряд из абсолютных величин
его членов:
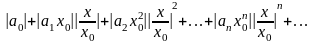Члены
этого ряда меньше соответствующих
членов ряда
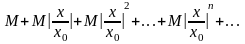
При
последний ряд представляет собой
геометрическую прогрессию со знаменателем
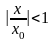и, следовательно, сходится.
Теперь
нетрудно доказать и вторую часть
теоремы: пусть в некоторой точке
ряд
расходится. Тогда он будет расходиться
в любой точке х, удовлетворяющей условию
.
Действительно, если бы в какой-либо
точке х-, удовлетворяющей этому условию,
ряд сходился, то в силу только что
доказанной первой части теоремы он
должен был бы сходиться и в точке
,
так как
.
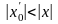Но это противоречит условию, что в точке
ряд расходится. Следовательно, ряд
расходится и в точке х. Теорема полностью
доказана.
Интервалом сходимости степенного ряда является такой интервал от –R до R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для
19. Радиус сходимости.
Радиусом сходимости назовем такое R , что при всех х, таких что |x|<R ряд сходится, а при всех х, |x|>R, ряд расходится. (-R, R) – интервал сходимости.
Замечание: при |x|<R ряд сходится абсолютно. В точке x=R x=-R надо исследовать отдельно.
Нахождение радиуса сходимости.
Составим ряд из модулей данного ряда и применим к нему признак Даламбера. Найдем предел (U(n+1)/Un). Ряд сходится при |x|<lim(an/a(n+1); расходится при |x|>lim(an/a(n+1);
точек х, лежащих вне его, ряд расходится. Число R называют радиусом сходимости степенного ряда.