
- •Свойства степенной функции с нечетным отрицательным показателем.
- •Свойства степенной функции с четным отрицательным показателем.
- •Свойства степенной функции с положительным рациональным показателем меньшим единицы.
- •Свойства степенной функции с положительным рациональным показателем большим единицы.
- •Свойства степенной функции с положительным рациональным показателем большим единицы.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства показательной функции с основанием меньшим единицы.
- •3.Логарифмические ,
- •Свойства логарифмической функции с основанием меньшим единицы.
- •Свойства функции логарифма с основанием большим единицы.
- •4.Тригонометрические
- •5.Обратные тригонометрические (аркфункции)
5.Обратные тригонометрические (аркфункции)
◦Функция
арксинус y=arcsin(x)
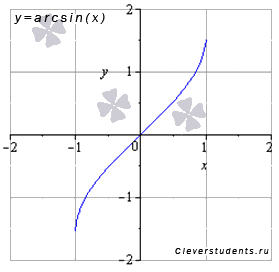
Свойства функции y=arcsin(x).
◦Область
определения арксинуса:
![]()
◦Область
значений функции арксинус:
![]() .
.
◦Функция нечетная, так как .
◦Функция возрастает на всей области определения, то есть, при .
◦Функция
вогнутая при
![]() ,
выпуклая при
,
выпуклая при
![]() .
.
◦Точка перегиба (0; 0) , она же ноль функции.
◦Асимптот нет.
◦Функция
арккосинус y=arccos(x) 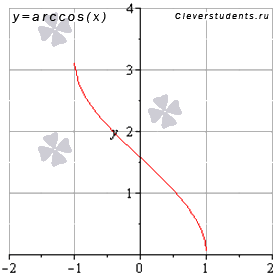
Свойства функции y=arccos(x).
◦Область определения арккосинуса:
◦Область
значений арккосинуса:
![]() .
.
◦Функция не является ни четной ни нечетной, то есть, она общего вида.
◦Функция убывает на всей области определения, то есть, при
◦Функция вогнутая при , выпуклая при
◦Точка
перегиба
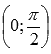 .
.
◦Асимптот нет.
◦Функция
арктангенс y=arctg(x) 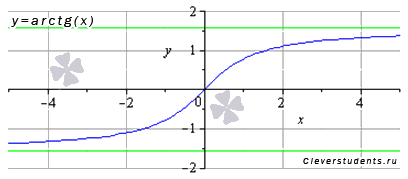
Свойства функции y=arctg(x).
◦Область определения: .
◦Область
значений:
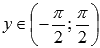 .
.
◦Функция арктангенс - нечетная, так как .
◦Функция возрастает на всей области определения, то есть, при .
◦Функция арктангенс вогнутая при , выпуклая при .
◦Точка перегиба (0; 0) , она же ноль функции.
◦Горизонтальными
асимптотами являются прямые
![]() при
при
![]() и
и
![]() при
при
![]() .
На чертеже они показаны зеленым цветом.
.
На чертеже они показаны зеленым цветом.
◦Функция
арккотангенс y=arcctg(x)
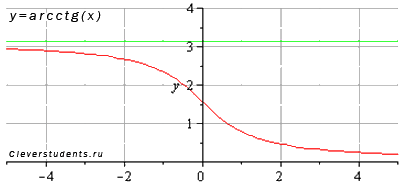
Свойства функции y=arcctg(x).
◦Область определения: .
◦Область
значений арккотангенса:
![]() .
.
◦Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
◦Функция убывает на всей области определения, то есть, при .
◦Функция вогнутая при , выпуклая при .
◦Точка перегиба .
◦Горизонтальными
асимптотами являются прямые
![]() при
(на чертеже показана зеленым цветом) и
y=0 при
.
при
(на чертеже показана зеленым цветом) и
y=0 при
.
Преобразование графиков элементарных функций.
Три способа геометрических преобразований графика функции:
•Масштабирование (сжатие или растяжение) вдоль осей абсцисс и ординат.
На
необходимость масштабирования указывают
коэффициенты k1
и k2
отличные от единицы, если
![]() ,
то происходит сжатие графика относительно
oy и растяжение относительно ox , если
,
то происходит сжатие графика относительно
oy и растяжение относительно ox , если
![]() ,
то производим растяжение вдоль оси
ординат и сжатие вдоль оси абсцисс.
,
то производим растяжение вдоль оси
ординат и сжатие вдоль оси абсцисс.
•Симметричное (зеркальное) отображение относительно координатных осей.
На необходимость этого преобразования указывают знаки «минус» перед коэффициентами k1 (в этом случае симметрично отображаем график относительно оси ox ) и k2 (в этом случае симметрично отображаем график относительно оси oy ). Если знаков «минус» нет, то этот шаг пропускается.
•Параллельный перенос (сдвиг) вдоль осей ox и oy .
Это преобразование производится В ПОСЛЕДНЮЮ ОЧЕРЕДЬ при наличии коэффициентов a и b , отличных от нуля. При положительном а график сдвигается влево на а единиц, при отрицательных а – вправо на а единиц. При положительном b график функции параллельно переносим вверх на b единиц, при отрицательном b – вниз на b единиц.
Пример (преобразование графика степенной функции).
С
помощью преобразования графика функции
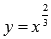 построить
построить
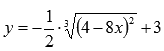
Решение.
Функция представляется в следующем виде:
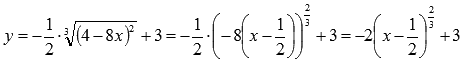
Имеем k1=2, причем перед этим коэффициентом знак «минус»,
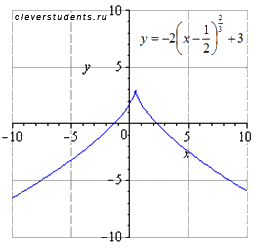
а=-1/2 , b=3 . Следовательно, получили цепочку геометрических преобразований графика: растяжение вдоль оси ординат вдвое, симметричное отображение относительно оси абсцисс, сдвиг вправо на 1/2 и сдвиг вверх на 3 единицы.
исходная степенная функция
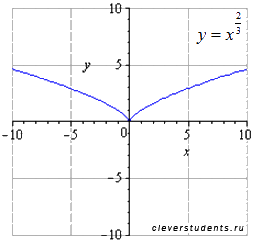
растягиваем вдоль оси oy вдвое
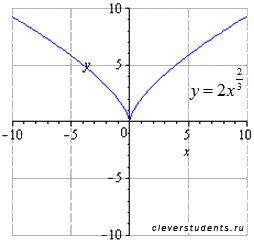
отображаем симметрично относительно оси ox
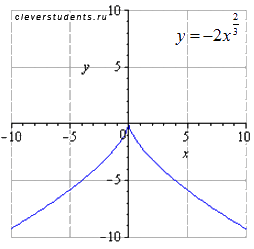
сдвигаем вправо на 1/2
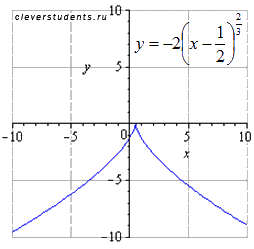
сдвигаем вверх на 3 единицы
Пример (преобразование графика показательной функции).
Построить
график показательной функции
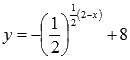
Решение.
По свойствам степени преобразуем функцию:
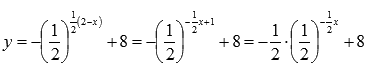
Таким
образом, имеем цепочку преобразований
графика показательной функции :
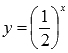
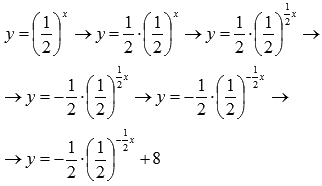
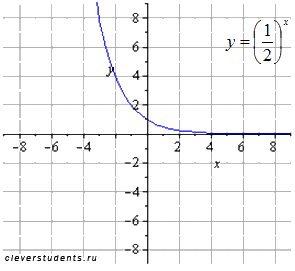
исходная показательная функция
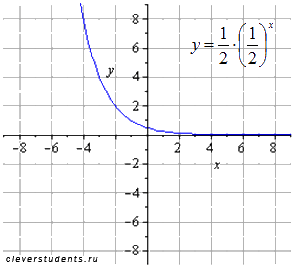
сжимаем вдоль оси oy вдвое
растягиваем вдвое вдоль оси ox
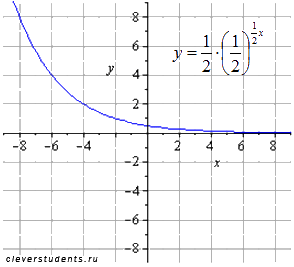
отображаем симметрично относительно оси ox
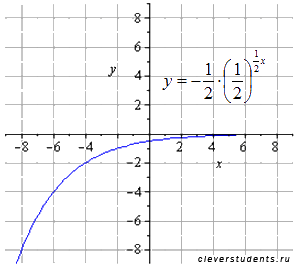
отображаем симметрично относительно оси oy
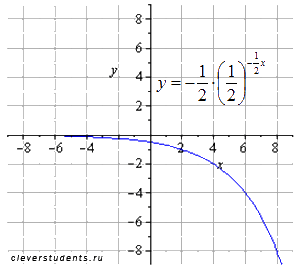
сдвигаем вверх на 8 единиц
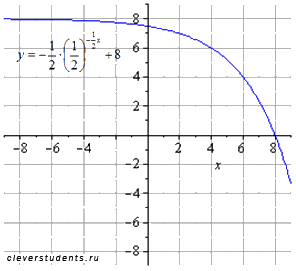
Пример (геометрические преобразования графика логарифмической функции y=ln(x)).
Построить
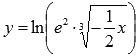 преобразованием графика функции
преобразованием графика функции
![]()
Решение.
Используем свойства логарифма:
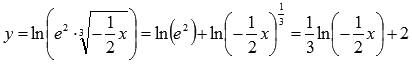
Таким образом, имеем цепочку преобразований графика логарифмической функции:
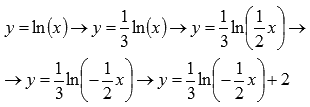
график исходной функции натуральный логарифм
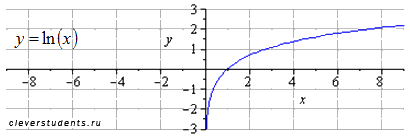
сжимаем вдоль оси oy втрое
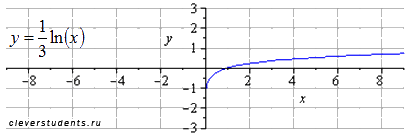
растягиваем вдвое вдоль оси ox
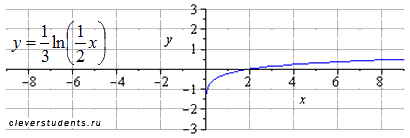
отображаем симметрично относительно оси oy
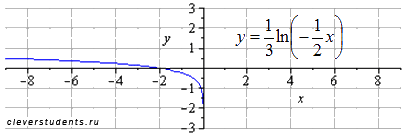
сдвигаем вверх на 2 единицы
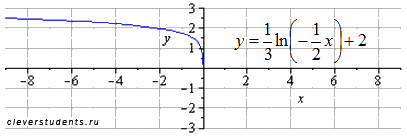
Преобразование
графиков тригонометрических функций
подчиняется общей схеме геометрических
преобразований
![]() .
Единственно хочется обратить внимание
на влияние коэффициента k2
на период тригонометрических функций.
При отличном от единицы коэффициенте
k2
период становится равным
.
Единственно хочется обратить внимание
на влияние коэффициента k2
на период тригонометрических функций.
При отличном от единицы коэффициенте
k2
период становится равным
![]() .
То есть, при
.
То есть, при
![]() растяжение графика функции вдоль оси
абсцисс соответствует увеличению
периода, а при
растяжение графика функции вдоль оси
абсцисс соответствует увеличению
периода, а при
![]() сжатие графика соответствует уменьшению
периода. Коэффициент k1
влияет на амплитуду колебаний синусоиды
и косинусоиды.
сжатие графика соответствует уменьшению
периода. Коэффициент k1
влияет на амплитуду колебаний синусоиды
и косинусоиды.
Пример (геометрические преобразования синусоиды y=sinx).
С помощью преобразования графика функции y=sinx построить
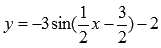
Решение.
Приводим функцию к виду шаблона :
![]()
Имеем k1=3, k2=0,5, a=3, b=-2, причем перед коэффициентом k1 стоит знак «минус», перед k2 минуса нет.
Таким образом, цепочка преобразований графика функции y=sinx примет вид:
Поэтапное преобразование графика синусоиды. Графическая иллюстрация.
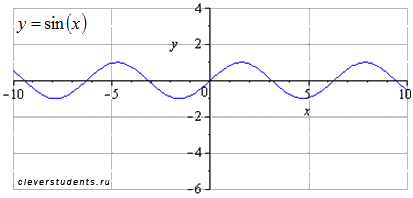
График исходной синусоиды y=sin(x) . Наименьший положительный период равен . Максимумы находятся в точках , минимумы – в точках .
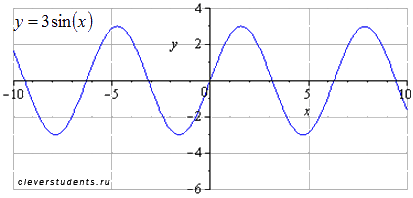
Растягиваем
вдоль оси ординат втрое (амплитуда
колебаний при этом возрастает в три
раза). Наименьший положительный период
равен
.
Максимумы переходят в точки
![]() ,
минимумы – в точки
,
минимумы – в точки
![]() .
.
Растягиваем
вдоль оси абсцисс вдвое. Наименьший
положительный период при этом вдвое
увеличивается
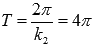 .
Максимумы переходят в точки
.
Максимумы переходят в точки
![]() ,
минимумы – в точки
,
минимумы – в точки
![]() .
.
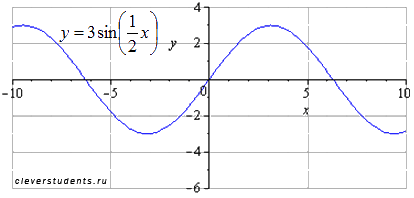
Симметрично
отображаем относительно оси абсцисс.
Наименьший положительный период при
этом не меняется
![]() .
Максимумы переходят в точки
.
Максимумы переходят в точки
![]() ,
минимумы – в точки
,
минимумы – в точки
![]() .
.
С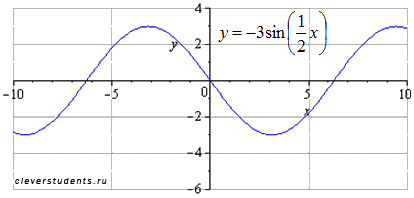 двигаем
график вправо на 3 единицы. Наименьший
положительный период при этом не меняется
.
Максимумы переходят в точки
двигаем
график вправо на 3 единицы. Наименьший
положительный период при этом не меняется
.
Максимумы переходят в точки
![]() ,
минимумы – в точки
,
минимумы – в точки
![]() .
.
С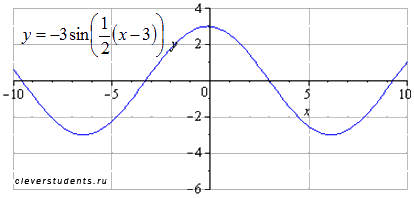 двигаем
график вниз на 2 единицы. Наименьший
положительный период при этом не меняется
.
Максимумы переходят в точки
двигаем
график вниз на 2 единицы. Наименьший
положительный период при этом не меняется
.
Максимумы переходят в точки
![]() минимумы – в точки
минимумы – в точки
![]()
Э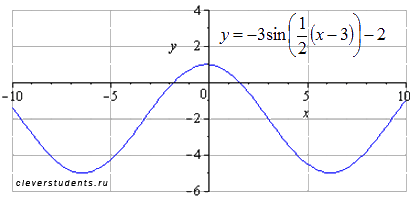 тим
этапом задача преобразования графика
тригонометрической функции y=sinx
завершается.
тим
этапом задача преобразования графика
тригонометрической функции y=sinx
завершается.
Пример (преобразование тригонометрической функции y=cosx).
Построить
график функции
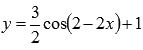 преобразованием косинусоиды y=cosx.
преобразованием косинусоиды y=cosx.
Решение.
Приводим функцию к виду шаблона :
![]()
Имеем
![]() ,
причем перед коэффициентом k2
стоит знак «минус», перед k1
минуса нет.
,
причем перед коэффициентом k2
стоит знак «минус», перед k1
минуса нет.
Таким образом, цепочка преобразований графика тригонометрической функции косинус примет вид:
Поэтапное преобразование графика косинусоиды. Графическая иллюстрация.
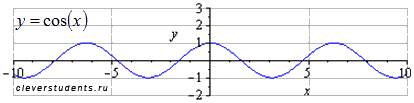
Исходный
график y=cos(x) . Наименьший положительный
период равен
.
Максимумы находятся в точках
![]() ,
минимумы – в точках
,
минимумы – в точках
![]() .
.
Растягиваем
вдоль оси ординат в 3/2 раза (амплитуда
колебаний при этом возрастает в 3/2 раза).
Наименьший положительный период равен
.
Максимумы переходят в точки
 ,
минимумы – в точки
,
минимумы – в точки
 .
.
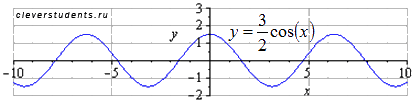
Сжимаем
график вдоль оси абсцисс вдвое. Наименьший
положительный период при этом вдвое
уменьшается
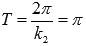 .
Максимумы переходят в точки
.
Максимумы переходят в точки
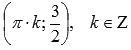 ,
минимумы – в точки
,
минимумы – в точки
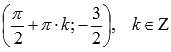 .
.
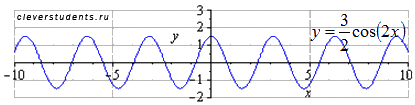
Симметрично отображаем относительно оси ординат. В силу четности функции график при этом не изменится.
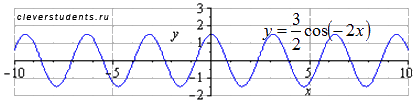 Сдвигаем
график вправо на 1 единицу. Наименьший
положительный период при этом не меняется
.
Максимумы переходят в точки
Сдвигаем
график вправо на 1 единицу. Наименьший
положительный период при этом не меняется
.
Максимумы переходят в точки
![]() , минимумы – в точки
, минимумы – в точки
![]() .
.
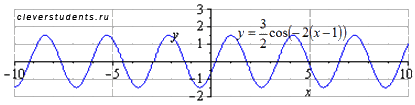
Сдвигаем
график вверх на 1 единицу. Наименьший
положительный период при этом не меняется
.
Максимумы переходят в точки
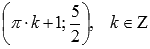 ,
минимумы – в точки
,
минимумы – в точки
![]() .
.
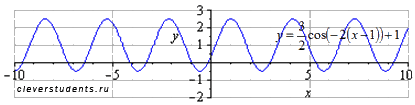
Этим этапом задача преобразования графика тригонометрической функции y=cosx завершается.
Пример (преобразование тригонометрической функции y=tgx ).
С
помощью геометрических преобразований
графика функции y=tgx построить
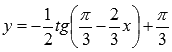
Решение.
Приводим функцию к виду шаблона :
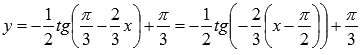
Имеем
![]() ,
причем перед коэффициентами k1
и k2
стоит знак «минус».
,
причем перед коэффициентами k1
и k2
стоит знак «минус».
Таким образом, цепочка преобразований графика тангенсоиды примет вид:
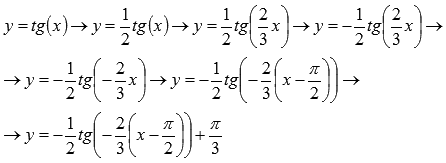
Поэтапное преобразование графика тангенсоиды. Графическая иллюстрация.
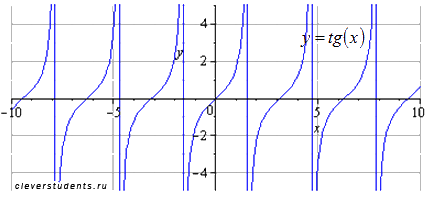
Исходный
график y=tg(x) . Наименьший положительный
период равен
.
Область определения
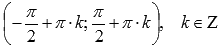 .
.
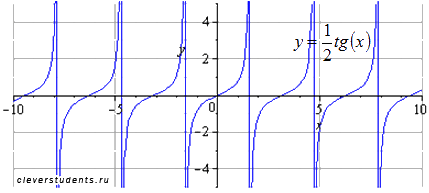
Производим сжатие вдоль оси ординат в 2 раза. Наименьший положительный период при этом не меняется . Область определения остается прежней .
Растягиваем
график вдоль оси абсцисс в 3/2 раза.
Наименьший положительный период при
этом равен
![]() .
Область определения изменяется на
.
Область определения изменяется на
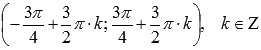 .
.
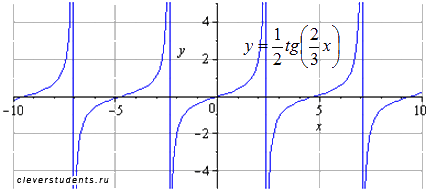
Симметрично отображаем относительно оси абсцисс. Период и область определения при этом не меняются.
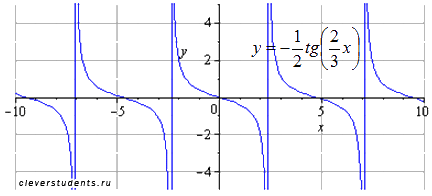
Симметрично отображаем относительно оси ординат. Период и область определения при этом не меняются. Стоит заметить, что график в точности совпадает с графиком двумя шагами ранее. Это объясняется нечетностью функции тангенса. То есть, если к нечетной функции применить симметричное отображение относительно осей ox и oy , то получим исходную функцию.
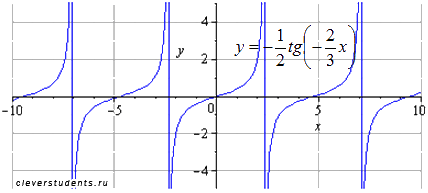
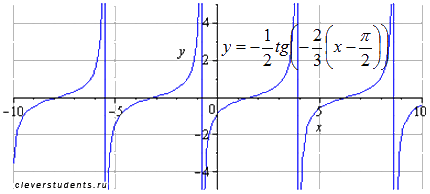
Сдвигаем
график вправо на
![]() (примерно на полторы единицы). Наименьший
положительный период при этом не меняется
(примерно на полторы единицы). Наименьший
положительный период при этом не меняется
![]() Область
определения изменяется на
Область
определения изменяется на
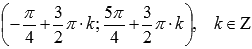 .
.
Сдвигаем
график вверх на
![]() (примерно на единицу). Период и область
определения при этом не меняются.
(примерно на единицу). Период и область
определения при этом не меняются.
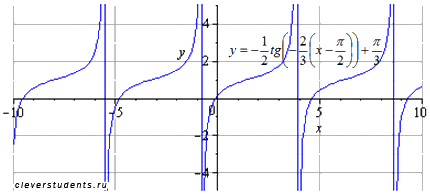
Этим этапом задача преобразования графика тригонометрической функции y=tgx завершается.
Пример (геометрические преобразования обратной тригонометрической функции y=arccosx).
Построить
график функции
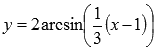 преобразованием графика y=arccosx.
преобразованием графика y=arccosx.
Решение.
Сначала от арккосинуса перейдем к арксинусу, используя соотношение обратных тригонометрических функций
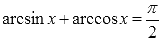
Следовательно,
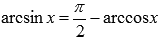
Таким образом, имеем цепочку преобразований арккосинуса в арксинус:
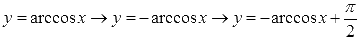
Поэтапное преобразование графика арккосинуса. Графическая иллюстрация.
Исходный график y=arccos(x) .
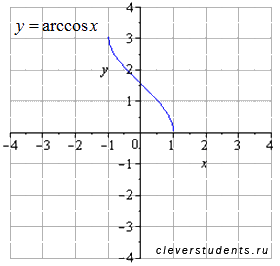
Отображаем симметрично относительно оси ox .
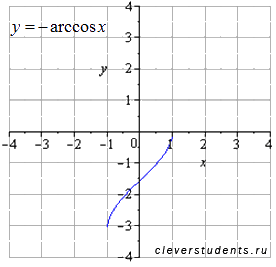
Сдвигаем вверх на .
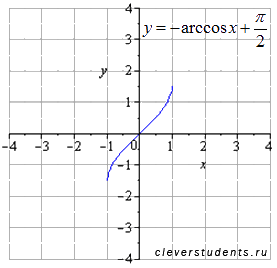
Вот так перешли от арккосинуса к арксинусу
Теперь проводим геометрические преобразования графика арксинуса.
Имеем
![]() ,
причем перед коэффициентами k1и
k2
знака минуса нет.
,
причем перед коэффициентами k1и
k2
знака минуса нет.
Таким образом, цепочка преобразований графика y=arcsinx примет вид:
Поэтапное преобразование графика арксинуса. Графическая иллюстрация.
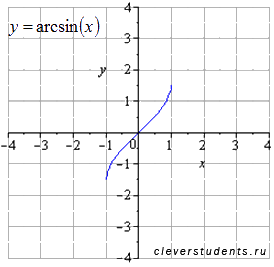
График
функции y=arcsinx . Область определения
![]() .
Область значений
.
Область значений
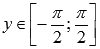 .
.
Растягиваем
вдвое вдоль оси ординат. Область
определения не меняется
.
Область значений становится
![]() .
.
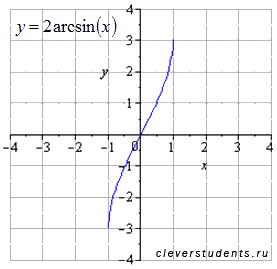
Растягиваем
вдоль оси абсцисс втрое. При этом область
определения расширяется до
![]() .
Область значений не меняется
.
.
Область значений не меняется
.
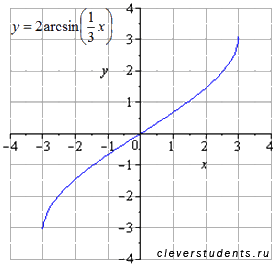
Сдвигаем
график на единицу вправо. При этом
область определения переходит в
![]() .
Область значений не меняется
.
.
Область значений не меняется
.
Э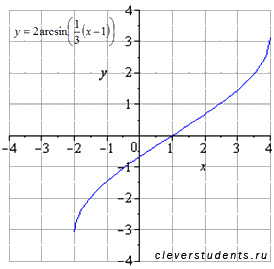 тим
этапом задача преобразования графика
обратной тригонометрической функции
завершается.
тим
этапом задача преобразования графика
обратной тригонометрической функции
завершается.
