
- •Свойства степенной функции с нечетным отрицательным показателем.
- •Свойства степенной функции с четным отрицательным показателем.
- •Свойства степенной функции с положительным рациональным показателем меньшим единицы.
- •Свойства степенной функции с положительным рациональным показателем большим единицы.
- •Свойства степенной функции с положительным рациональным показателем большим единицы.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства степенной функции с отрицательным рациональным показателем.
- •Свойства показательной функции с основанием меньшим единицы.
- •3.Логарифмические ,
- •Свойства логарифмической функции с основанием меньшим единицы.
- •Свойства функции логарифма с основанием большим единицы.
- •4.Тригонометрические
- •5.Обратные тригонометрические (аркфункции)
27.Элементарные функции. Их свойства. Построение графиков функций с помощью элем-ных преобразований.
Основные элементарные функции, их свойства и графики.
1.Степенные y= x a с целым показателем.
ЗАМЕЧАНИЯ:
1.к основным элементарным степенным функциям относят лишь степенные функции С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
2. неограничивание области определения интервалом .
I.Пусть а=1, 3, 5, … , то есть а – нечетное.
В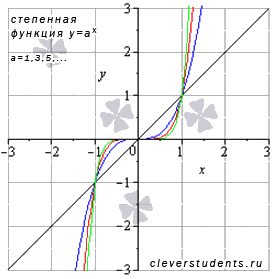 этом случае график степенной функции
будет иметь вид:
этом случае график степенной функции
будет иметь вид:
В качестве примера взяты а=1 – черная линия, а=3 – синяя линия, а=5 – красная линия, а=7 – зеленая линия. При а=1 имеем линейную функцию y=x - частный случай степенной.
Свойства степенной функции с нечетным положительным показателем.
◦Область определения: x € (-∞;+∞).
◦Область значений: y € (-∞;+∞).
◦Функция нечетная, так как y(-x)=-y(x) .
◦Функция возрастает при x € (-∞;+∞).
◦Функция выпуклая при x € (-∞;0] и вогнутая при x € [0;+∞)
(кроме линейной функции).
◦Точка (0;0) является точкой перегиба (кроме линейной функции).
◦ Асимптот
нет.
Асимптот
нет.
◦Функция проходит через точки (-1;-1) , (0;0), (1;1) .
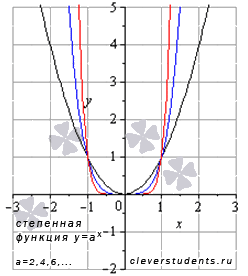
II.Пусть а=2, 4, 6, … , то есть а – четное.
В этом случае график степенной функции будет иметь вид:
В качестве примера взяты а=2 – черная линия, а=4 – синяя линия, а=8 – красная линия. При а=2 имеем квадратичную функцию – квадратичную параболу – частный случай степенной.
Свойства степенной функции с четным положительным показателем.
◦Область определения: x € (-∞;+∞)
◦Область значений: y € [0;+∞)
◦Функция четная, так как y(-x)=y(x).
◦Функция возрастает при x € [0;+∞)., убывает при x € (-∞;0]
◦Функция вогнутая при x € (-∞;+∞).
◦Точек перегиба нет.
◦Асимптот нет.
◦Функция проходит через точки (-1;1) , (0;0) , (1;1) .
III.Пусть а=-1, -3, -5, …
В
этом случае график степенной функции
будет иметь вид: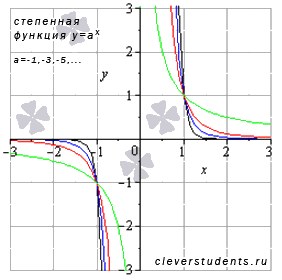
В качестве примера взяты а=-9 – черная линия, а=-5 – синяя линия, а=-3 – красная линия, а=-1 – зеленая линия. При а=-1 имеем обратную пропорциональность ( гиперболу ) - частный случай степенной.
Свойства степенной функции с нечетным отрицательным показателем.
◦Область определения: x € (-∞;0) U x € (0;+∞). При x=0 имеем разрыв второго рода, так как
Lim(x→0-0) xa = -∞, lim (x→0+0) xa = +∞,при а=-1, -3, -5, …. Следовательно, прямая x=0 является вертикальной асимптотой.
◦Область значений: y € (-∞;0) U € (0;+∞).
◦Функция нечетная, так как y(-x)=-y(x).
◦Функция убывает при x € (-∞;0)U (0;+∞).
◦Функция выпуклая при x € (-∞;0) и вогнутая при x € (0;+∞).
◦Точек перегиба нет.
◦Горизонтальной асимптотой является прямая y=0 , так как
k= lim(x→∞) xa/x =0, b= lim(x→∞) xa-kx = 0
y=kx+b = 0 при а=-1, -3, -5, … .
◦Функция проходит через точки (-1;-1) , (1;1) .
IV.Пусть а=-2, -4, -6, …
В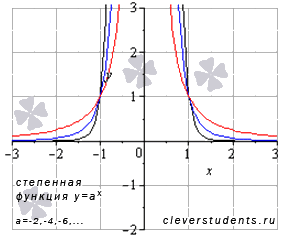 этом случае график степенной функции
будет иметь вид:
этом случае график степенной функции
будет иметь вид:
В качестве примера взяты а=-8 – черная линия, а=-4 – синяя линия, а=-2 – красная линия.
Свойства степенной функции с четным отрицательным показателем.
◦Область определения: x € (-∞;0)U (0;+∞).
При x=0 имеем разрыв второго рода, так как
Lim(x→0-0) xa = +∞, Lim(x→0+0) xa = +∞ при а=-2, -4, -6, … . Следовательно, прямая x=0 является вертикальной асимптотой.
◦Область значений: y € (0;+∞) .
◦Функция четная, так как y(-x)=y(x).
◦Функция возрастает при x € (-∞;0), убывает при x€ (0;+∞)
◦Функция вогнутая при x € (-∞;0)U(0;+∞).
◦Точек перегиба нет.
◦Горизонтальной асимптотой является прямая y=0 , так как
L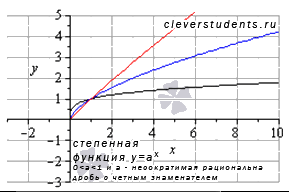 im(x→∞)
xa
/x=
0, Lim(x→0+0)
(xa-kx)
= 0
im(x→∞)
xa
/x=
0, Lim(x→0+0)
(xa-kx)
= 0
y=kx+b+0 при а=-2, -4, -6, … .
◦Функция проходит через точки (-1;1) , (1;1) .
V.Пусть 0<a<1 и а – несократимая рациональная дробь с четным знаменателем (например, а=1/4 или 3/8 ).
В этом случае график степенной функции будет иметь вид:
В качестве примера взяты а=1/4 – черная линия, а=5/8 – синяя линия, а=11/12 – красная линия.
Свойства степенной функции с положительным рациональным показателем меньшим единицы.
◦Область определения:x€[0;+∞) .
◦Область значений: y€[0;+∞).
◦Функция не является ни четной, ни нечетной, то есть она общего вида.
◦Функция возрастает при x€[0;+∞) .
◦Функция выпуклая при x€[0;+∞).
◦Точек перегиба нет.
◦Асимптот нет.
◦Функция проходит через точки (0;0) , (1;1) .
Замечание.
Если 0<a<1 и а – иррациональное число, то вид графика степенной функции аналогичен рассмотренным в этом пункте, свойства степенной функции с иррациональным показателем абсолютно схожи.
Замечание о важности несократимости рациональной дроби в показателе степени.
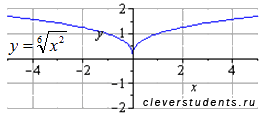
графики функций y=x2/6 и y=x1/3 не есть одно и то же, если не оговорен момент о несократимости показателя степени . Этим мы НЕ ХОТИМ сказать, что 2/6=/ 1/3, но y=x2/6 можно трактовать по-разному, y= x2/6 = (6корней х)2 или y= x2/6 = (6корней х2) . Удивительно, ни первая, ни вторая функция не соответствуют y=x1/3.
В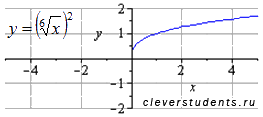 от
тому графическая иллюстрация:
от
тому графическая иллюстрация:

В дальнейшем y=xm/n будем рассматривать как y= (n корней из xm)
V I.Пусть
0<a<1
и если числитель и знаменатель
рациональной дроби в показателе степени
представляет собой нечетные числа, а
сама дробь несократима (например, 1/3 или
5/7), то областью определения такой функции
принято считать все действительные
числа
I.Пусть
0<a<1
и если числитель и знаменатель
рациональной дроби в показателе степени
представляет собой нечетные числа, а
сама дробь несократима (например, 1/3 или
5/7), то областью определения такой функции
принято считать все действительные
числа
![]() ,
и область значений будет
,
и область значений будет
![]() .
.
График степенной функции в этом случае будет иметь вид, схожий с:
В качестве примера взяты а=1/3 – синяя линия, а=5/7 – красная линия.
Свойства степенной функции с положительным рациональным показателем меньшим единицы.
◦Область определения: .
◦Область значений: .
◦Функция
нечетная, так как
![]() .
.
◦Функция возрастает при .
◦Функция
вогнутая при
![]() и выпуклая при
и выпуклая при
![]() .
.
◦Точка (0;0) является точкой перегиба.
◦Асимптот нет.
◦Функция проходит через точки (-1;-1) , (0;0) , (1;1) .
V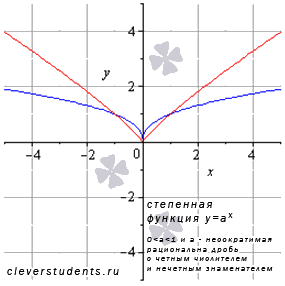 II.Пусть
II.Пусть
![]() и
если числитель рациональной дроби в
показателе степени представляет собой
четное число, а знаменатель - нечетное
число и сама дробь несократима (например,
2/3 или 6/7 ), то областью определения такой
функции принято считать все действительные
числа
,и
область значений будет
и
если числитель рациональной дроби в
показателе степени представляет собой
четное число, а знаменатель - нечетное
число и сама дробь несократима (например,
2/3 или 6/7 ), то областью определения такой
функции принято считать все действительные
числа
,и
область значений будет
![]() .
.
График степенной функции в этом случае будет иметь вид, схожий с:
В качестве примера взяты а=2/5 – синяя линия, а=6/7 – красная линия.
