
- •3. Вычисление двойного интеграла в декартовых координатах
- •2. Свойства двойного интеграла
- •12. Функции комплексного переменного: определение, геометрический смысл. Предел и непрерывность функции комплексного переменного.
- •13. Дифференцируемость, производная фкп. Геометрический смысл производной.
- •14. Условие Коши – Римана. Понятие аналитической функции.
- •15. Функция ez и ее свойства.
- •18. Связь между аналитическими и гармоническими функциями.
1.
Двойной интеграл: определение, теорема
существования, геометрический и
механический смысл. Пусть
в замкнутой квадрируемой области
![]() плоскости
XOY
задана функция f(x;y).
Разобьем область
произвольно
на n
частей
плоскости
XOY
задана функция f(x;y).
Разобьем область
произвольно
на n
частей
![]() так
чтобы области
не
имели общих внутренних точек. В каждой
замкнутой области
так
чтобы области
не
имели общих внутренних точек. В каждой
замкнутой области
![]() (внутри
или на границе) выберем произвольную
точку
(внутри
или на границе) выберем произвольную
точку
![]() и
умножим значение функции
f(x;y)
в этой точке на площадь
.
Сложив все такие произведения, получим
сумму:
и
умножим значение функции
f(x;y)
в этой точке на площадь
.
Сложив все такие произведения, получим
сумму:
![]() которая
называется интегральной суммой для
функции
f(x;y) в
области
.
Обозначим
через 𝛌 шаг
разбиения области
на
части
которая
называется интегральной суммой для
функции
f(x;y) в
области
.
Обозначим
через 𝛌 шаг
разбиения области
на
части
![]() .
Процесс, состоящий в неограниченном
измельчении областей деления и
соответственно в неограниченном
увеличении числа n
областей деления, удобно характеризовать
словами: «шаг разбиения области
стремится
к нулю». Если при стремлении к нулю шага
разбиения
.
Процесс, состоящий в неограниченном
измельчении областей деления и
соответственно в неограниченном
увеличении числа n
областей деления, удобно характеризовать
словами: «шаг разбиения области
стремится
к нулю». Если при стремлении к нулю шага
разбиения
![]() области
интегральные
суммы (1) имеют предел, то этот предел
называют двойным интегралом от функции
области
интегральные
суммы (1) имеют предел, то этот предел
называют двойным интегралом от функции
![]() по
области
и
обозначают символами:
по
области
и
обозначают символами:
![]() или
или ![]() .
.
Теорема.
Если функция
f(x,
y)
непрерывна в замкнутой области ,
то двойной интеграл
![]() существует.
Теорема.
Если функция
f(x,
y)
ограничена в замкнутой области
и непрерывна в ней всюду, кроме конечного
числа кусочно – гладких линий, то
двойной интеграл существует.
Геометрический
смысл: Если
f(x:y)
> 0, то двойной интеграл от функции z
= f(x:y)
по области S
равен объему тела, ограниченного сверху
поверхностью z
= f(x:y),
с боков – цилиндрической поверхностью,
снизу – плоскостью z
= 0. Механический
смысл: Двойной
интеграл от функции z
= f(x:y)
> 0 по области S
представляет собой массу фигуры S,
если подынтегральную функцию f(x:y)
считать плотностью этой фигуры в точке
M(x:y).
существует.
Теорема.
Если функция
f(x,
y)
ограничена в замкнутой области
и непрерывна в ней всюду, кроме конечного
числа кусочно – гладких линий, то
двойной интеграл существует.
Геометрический
смысл: Если
f(x:y)
> 0, то двойной интеграл от функции z
= f(x:y)
по области S
равен объему тела, ограниченного сверху
поверхностью z
= f(x:y),
с боков – цилиндрической поверхностью,
снизу – плоскостью z
= 0. Механический
смысл: Двойной
интеграл от функции z
= f(x:y)
> 0 по области S
представляет собой массу фигуры S,
если подынтегральную функцию f(x:y)
считать плотностью этой фигуры в точке
M(x:y).
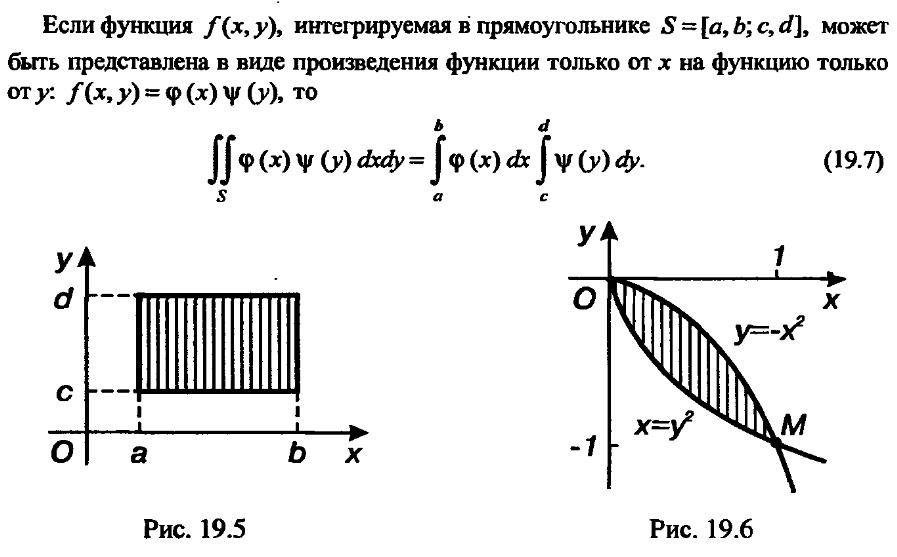
3. Вычисление двойного интеграла в декартовых координатах


2. Свойства двойного интеграла
![]() откуда
откуда
![]()
4.
Двойной интеграл в полярных координатах.
Пусть
область D ограничена линией r
= r() и лучами
= и
= ,
где и r
– полярные координаты точки на плоскости,
связанные с ее декартовыми координатами
x
и y
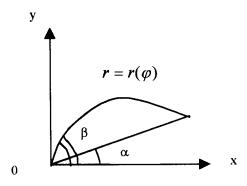 Рис. 5
соотношениями
Рис. 5
соотношениями![]() (рис. 5). В этом случае
(рис. 5). В этом случае
 Замечание.
Если область
D в декартовых координатах задается
уравнением, содержащим бином
Замечание.
Если область
D в декартовых координатах задается
уравнением, содержащим бином
![]() ,
например,
,
например,
![]() и
т.д., то вычисление двойного интеграла
по такой области удобнее производить
в полярных координатах.
и
т.д., то вычисление двойного интеграла
по такой области удобнее производить
в полярных координатах.
5. Геометрические
и механические приложения двойного
интеграла.
Вычисление
площадей плоских фигур![]() Пример:
Пример:![]() Определим
точки пересечения кривых: х-2-x2
x2+
х - 2 = О,
Определим
точки пересечения кривых: х-2-x2
x2+
х - 2 = О,
![]() =
-2;1;
=
-2;1;![]() (-2,-2),
(-2,-2),![]() (1,
1) (рис. 23.9).
(1,
1) (рис. 23.9).![]()
 Рис.
23.9
Рис.
23.9 Вычисление объемов
цилиндрических тел
Вычисление объемов
цилиндрических тел![]() (см.
разд. 23.1).Пример:
(см.
разд. 23.1).Пример:![]() (рис. 23.11). V = ?
(рис. 23.11). V = ?![]()
![]()
Замечание. Если
тело, объем которого нужно найти,
ограничено сверху поверхностью![]() а
снизу
а
снизу![]() причем
проекцией обеих поверхностей на
плоскость XOY является область D, то объем
V этого тела (рис. 23.11) вычисляется по
формуле
причем
проекцией обеих поверхностей на
плоскость XOY является область D, то объем
V этого тела (рис. 23.11) вычисляется по
формуле![]()
 Механические
приложения двойного интеграла
Пусть
в плоскости Oxy
есть материальная пластинка, то есть
некоторая область D,
по которой распределена масса с
плотностью μ(x,
y). Тогда:
масса
пластинки
Механические
приложения двойного интеграла
Пусть
в плоскости Oxy
есть материальная пластинка, то есть
некоторая область D,
по которой распределена масса с
плотностью μ(x,
y). Тогда:
масса
пластинки
![]() статические
моменты
относительно координатных осей:
статические
моменты
относительно координатных осей:![]() ,
,
![]() координаты
(xc,
yc)
центра
масс
пластинки:
координаты
(xc,
yc)
центра
масс
пластинки:
![]() ,
,
![]()
6.
Тройной интеграл: определение, теорема
существования, механический смысл,
свойства.
Определяется
аналогично двойному интегралу.
Пусть в пространстве Oxyz задана
ограниченная замкнутая область (объём)
V, и пусть на области V определена функция
f(x, y, z). Разобьём область V произвольным
образом на n подобластей V1, V2, V3, …, Vn,
(не имеющих общих внутренних точек).
Символом v(Vi) будем обозначать объём
области Vi; символом d обозначим наибольший
из диаметров областей Vi:
![]() .
В каждой из подобластей Vi (i = 1,2,…,n)
выберем произвольную точку Pi = (xi, yi,
zi), вычислим в этой точке значение
функции f(Pi ) = f (xi, yi, zi), и составим
интегральную сумму
.
В каждой из подобластей Vi (i = 1,2,…,n)
выберем произвольную точку Pi = (xi, yi,
zi), вычислим в этой точке значение
функции f(Pi ) = f (xi, yi, zi), и составим
интегральную сумму ![]() . Если
существует предел последовательности
интегральных сумм при
. Если
существует предел последовательности
интегральных сумм при
![]() ,
не зависящий ни от способа разбиения
области V на подобласти Vi, ни от выбора
точек Pi, то функция f(x, y, z) называется
интегрируемой по области V, а значение
этого предела называется тройным
интегралом от функции f(x, y, z)по области
V и обозначается
,
не зависящий ни от способа разбиения
области V на подобласти Vi, ни от выбора
точек Pi, то функция f(x, y, z) называется
интегрируемой по области V, а значение
этого предела называется тройным
интегралом от функции f(x, y, z)по области
V и обозначается
![]() .
Если расписать значение f(P) через
координаты точки P, и представить dv как
dv = dx dy dz, получим другое обозначение
тройного интеграла:
.
Если расписать значение f(P) через
координаты точки P, и представить dv как
dv = dx dy dz, получим другое обозначение
тройного интеграла:
![]() .
Итак, кратко,
.
Итак, кратко,
![]() Тройной
интеграл от функции U=f(x,y,z),
распространенным на область V,
называется предел соответствующей
трехкратной суммы.
Тройной
интеграл от функции U=f(x,y,z),
распространенным на область V,
называется предел соответствующей
трехкратной суммы. Теорема
существования тройного интеграла. Если
подынтегральная функция непрерывна
на области V,
то она интегрируема по этой области.
Механический
смысл. Если
функция
Теорема
существования тройного интеграла. Если
подынтегральная функция непрерывна
на области V,
то она интегрируема по этой области.
Механический
смысл. Если
функция
![]() непрерывна
в замкнутой области V, то тройной интеграл
непрерывна
в замкнутой области V, то тройной интеграл
![]() существует.
Решение задачи о массе области V
с помощью тройного интеграла запишется
в виде:
существует.
Решение задачи о массе области V
с помощью тройного интеграла запишется
в виде:![]() где
где
![]() - плотность распределения массы. В этом
и заключается механический смысл
тройного интеграла от неотрицательной
функции.
Свойства аналогичны двойным
интегралам.
- плотность распределения массы. В этом
и заключается механический смысл
тройного интеграла от неотрицательной
функции.
Свойства аналогичны двойным
интегралам.
7. Тройной
интеграл: вычисление, геометрические
и механические приложения.
Вычисление
тройных интегралов производится путем
последовательного вычисления интегралов
меньшей кратности. 1.
Предположим, что функция f(x,
y, z) непрерывна
в рассматриваемой области T.
Пусть сначала T
= [a, b; c, d; e, f] -
прямоугольный параллелепипед,
проектирующийся на плоскость yz
в прямоугольник R
= [c, d; e, f].
Тогда
![]() Заменяя
в (1) двойной интеграл повторным,
получим
Заменяя
в (1) двойной интеграл повторным,
получим![]() Вычисление
тройного интеграла сводится к
последовательному вычислению трёх
определённых интегралов. Если первые
два интеграла в (2) объединить в двойной,
то будем иметь
Вычисление
тройного интеграла сводится к
последовательному вычислению трёх
определённых интегралов. Если первые
два интеграла в (2) объединить в двойной,
то будем иметь![]() где
P = [a, b; c, d]
- проекция параллелепипеда T
на плоскость xy.
Заметим, что в этих случаях можно менять
роли переменных.
2. Пусть область T
заключена между плоскостями x
= a и x = b,
причём каждое сечение области T
плоскостью
где
P = [a, b; c, d]
- проекция параллелепипеда T
на плоскость xy.
Заметим, что в этих случаях можно менять
роли переменных.
2. Пусть область T
заключена между плоскостями x
= a и x = b,
причём каждое сечение области T
плоскостью![]() представляет
собой квадрируемую фигуру G(x)(рис.
1). Тогда
представляет
собой квадрируемую фигуру G(x)(рис.
1). Тогда![]() 3. Пусть
теперь тело T
представляет собой "цилиндрический
брус", ограниченный снизу и сверху,
соответственно, поверхностями z
= z1(x,
y) и z
= z2(x,
y), проектирующиеся
на плоскость xy
в некоторую квадрируемую фигуру G
(рис.2), z1(x,
y) и z2(x,
y) - непрерывны
в G.
Тогда
3. Пусть
теперь тело T
представляет собой "цилиндрический
брус", ограниченный снизу и сверху,
соответственно, поверхностями z
= z1(x,
y) и z
= z2(x,
y), проектирующиеся
на плоскость xy
в некоторую квадрируемую фигуру G
(рис.2), z1(x,
y) и z2(x,
y) - непрерывны
в G.
Тогда
![]() Если
G
= {(x,
y):
a
≤ x
≤b,
y1(x)
≤ y
≤ y2(x)},
то
Если
G
= {(x,
y):
a
≤ x
≤b,
y1(x)
≤ y
≤ y2(x)},
то
![]()
8. Криволинейные
интегралы первого рода:
определение,
теорема существования, механический
смысл, свойства, вычисление.
Пусть
кривая C
описывается векторной функцией
![]() ,
где переменная s
представляет собой длину
дуги
кривой (рисунок 1).
Если на кривой C
определена скалярная
функция
F,
то интеграл
,
где переменная s
представляет собой длину
дуги
кривой (рисунок 1).
Если на кривой C
определена скалярная
функция
F,
то интеграл
![]() называется
криволинейным
интегралом первого рода
от скалярной функции F
вдоль кривой C
и обозначается как
называется
криволинейным
интегралом первого рода
от скалярной функции F
вдоль кривой C
и обозначается как
![]() Криволинейный интеграл
Криволинейный интеграл
![]() существует,
если функция F
непрерывна на кривой C.
Свойства
криволинейного интеграла первого рода
Криволинейный
интеграл I рода обладает следующими
свойствами:
1.
Интеграл не зависит от ориентации
кривой;
2.
существует,
если функция F
непрерывна на кривой C.
Свойства
криволинейного интеграла первого рода
Криволинейный
интеграл I рода обладает следующими
свойствами:
1.
Интеграл не зависит от ориентации
кривой;
2.
![]() 3.Если
гладкая кривая C
задана параметрически соотношением
3.Если
гладкая кривая C
задана параметрически соотношением
![]() и
скалярная функция F
непрерывна на кривой C,
то
и
скалярная функция F
непрерывна на кривой C,
то
![]() 4.
Если C
является гладкой кривой в плоскости
Oxy,
заданной уравнением
4.
Если C
является гладкой кривой в плоскости
Oxy,
заданной уравнением
![]() ,
то
,
то
![]() 5. Если гладкая кривая
C
в плоскости Oxy
определена уравнением
5. Если гладкая кривая
C
в плоскости Oxy
определена уравнением
![]() ,
то
,
то
![]() 6. В полярных координатах
интеграл
6. В полярных координатах
интеграл
![]() выражается
формулой
выражается
формулой
![]() где
кривая C
задана в полярных координатах функцией
где
кривая C
задана в полярных координатах функцией
![]() .
Вычисление
Пусть l —
гладкая, спрямляемая кривая, заданная
параметрически (как в определении).
Пусть функция f(x.y.z)
определена и интегрируема вдоль кривой
l
в смысле криволинейного интеграла
первого рода. Тогда
.
Вычисление
Пусть l —
гладкая, спрямляемая кривая, заданная
параметрически (как в определении).
Пусть функция f(x.y.z)
определена и интегрируема вдоль кривой
l
в смысле криволинейного интеграла
первого рода. Тогда![]() .Здесь
точкой обозначена производная по t:
.Здесь
точкой обозначена производная по t:
![]() .
.
9.
Криволинейные интегралы второго рода:
определение,
теорема существования, механический
смысл, свойства, вычисление.
Вновь
рассмотрим кривую L, в каждой точке
которой задана функция f(M), и зададим
разбиение кривой на отрезки. Выберем
на каждом отрезке точку Mi и умножим
значе-ние функции в этой точке не на
длину i-го отрезка, как в случае
криволинейного инте-грала 1-го рода, а
на проекцию этого отрезка, скажем, на
ось Ох, то есть на разность
xi – xi-1 = Δxi. Составим из полученных
произведений интегральную сумму
![]() .Определение
10.2. Если существует конечный предел
при
.Определение
10.2. Если существует конечный предел
при
![]() интегральной
суммы
интегральной
суммы
![]() ,
не зависящий от способа разбиения
кривой на отрезки и выбора точек Mi, то
от называется криволинейным интегралом
второго рода от функции f(M) по кривой L
и обозначается
,
не зависящий от способа разбиения
кривой на отрезки и выбора точек Mi, то
от называется криволинейным интегралом
второго рода от функции f(M) по кривой L
и обозначается ![]() .
Подобным образом можно определить и
криволинейные интегралы 2-го рода вида
.
Подобным образом можно определить и
криволинейные интегралы 2-го рода вида![]() Определение
10.3. Если вдоль кривой L определены
функции P(M) = P(x, y, z), Q(M) = Q(x, y, z), R(M) = R(x, y,
z) и существуют интегралы
Определение
10.3. Если вдоль кривой L определены
функции P(M) = P(x, y, z), Q(M) = Q(x, y, z), R(M) = R(x, y,
z) и существуют интегралы![]() ,то
и их сумму называют криволинейным
интегралом второго рода (общего вида)
и полагают
,то
и их сумму называют криволинейным
интегралом второго рода (общего вида)
и полагают
![]()
![]() .
Свойства
1.
Линейность:
.
Свойства
1.
Линейность:![]() 2. Аддитивность:
2. Аддитивность:![]() 3. Монотонность: если
3. Монотонность: если
![]() на
Γ, то
на
Γ, то
![]() 4. Оценка модуля:
4. Оценка модуля:
![]() 5. Теорема о
среднем: если f
непрерывна на Γ, то
5. Теорема о
среднем: если f
непрерывна на Γ, то
![]() ,
такая что:
,
такая что:
![]() 6.
6.
![]()
10.
Формула Грина. Условия независимости
криволинейного интеграла от пути
интегрирования. Пусть
в плоскости Oxy
задана область R,
ограниченная замкнутой, кусочно-непрерывной
и гладкой кривой C.
Предположим, что в некоторой области,
содержащей R,
задана непрерывная векторная функция
![]() с непрерывными частными производными
первого порядка
с непрерывными частными производными
первого порядка
![]() .
Тогда справедлива формула
Грина
.
Тогда справедлива формула
Грина
![]() где символ
где символ
![]() указывает,
что кривая (контур) C
является замкнутой, и обход при
интегрировании вдоль этой кривой
производится против часовой стрелки.
Если
указывает,
что кривая (контур) C
является замкнутой, и обход при
интегрировании вдоль этой кривой
производится против часовой стрелки.
Если
![]() ,
то формула Грина принимает вид
,
то формула Грина принимает вид
![]() где
S
− это площадь области R,
ограниченной контуром C.
Пусть в области D
заданы непрерывные функции P(x,y)
и Q(х,y)
и M0M
- гладкая дуга, лежащая в области D.
Рассмотрим вопрос о независимости
интеграла
где
S
− это площадь области R,
ограниченной контуром C.
Пусть в области D
заданы непрерывные функции P(x,y)
и Q(х,y)
и M0M
- гладкая дуга, лежащая в области D.
Рассмотрим вопрос о независимости
интеграла
![]() от
формы пути интегрирования. Имеет место
следующая теорема. Теорема
3.3.
Пусть функции P,
Q, P'y,
Q'x
определены
и непрерывны в односвязной, ограниченной
замкнутой области D
плоскости Оху.
Тогда следующие четыре условия
равносильны между собой:
1)
от
формы пути интегрирования. Имеет место
следующая теорема. Теорема
3.3.
Пусть функции P,
Q, P'y,
Q'x
определены
и непрерывны в односвязной, ограниченной
замкнутой области D
плоскости Оху.
Тогда следующие четыре условия
равносильны между собой:
1)![]() ,
где L
- замкнутый контур в области D;
2) интеграл
не
зависит от формы пути интегрирования,
а зависит лишь от положения точек M0
и М;
3) Pdx
+ Qdy = dU
- полный дифференциал некоторой функции
U(x,y);
4)
,
где L
- замкнутый контур в области D;
2) интеграл
не
зависит от формы пути интегрирования,
а зависит лишь от положения точек M0
и М;
3) Pdx
+ Qdy = dU
- полный дифференциал некоторой функции
U(x,y);
4)
![]() в
каждой точке области D.
Идея доказательства этой теоремы:
показывается, что из условия 1→ условие
2 →условие 3 → условие 4 → условие 1.
в
каждой точке области D.
Идея доказательства этой теоремы:
показывается, что из условия 1→ условие
2 →условие 3 → условие 4 → условие 1.
11. Комплексные числа. Алгебраическая, тригонометрическая и показательные формы комплексного числа, связь между ними. Действия над комплексными числами. Комплексные числа — расширение множества вещественных чисел, обычно обозначается С. Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица.
Алгебраическая форма. Запись комплексного числа z в виде x + iy, {x, y є R}, называется алгебраической формой комплексного числа.
Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что i2 = − 1): (a + ib) + (c + id) = (a + c) + i(b + d).
Тригонометрическая форма. Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент φ (x = rcos φ, y = rsin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической формеz = r(cos φ + isin φ).
Показательная
форма. Также
может быть полезна показательная форма
записи комплексных чисел, тесно связанная
с тригонометрической через формулу
Эйлера: z = reiφ,
где eiφ —
расширение экспоненты для
случая комплексного показателя степени.
Отсюда вытекают следующие широко
используемые равенства: cosφ= ;
sinφ=
;
sinφ= .
.
Действие над комплексными числами.
Сравнение: a + bi = c + di означает, что a = c и b = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
Сложение: (a + bi) + (c + di) = (a + c) + (b + d)i.
Вычитание: (a + bi) − (c + di) = (a − c) + (b − d)i.
Умножение: (a+bi)*(c+di)=ac+bci+adi+bdi2=(ac-bd)+(bc+ad)i.
Деление:
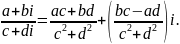
Извлечение
корня:
 .
.
 ,
k=0,1,…,n-1.
– формула Муара.
,
k=0,1,…,n-1.
– формула Муара.
