1.3. Таблица простейших определенных интегралов
Предполагается, что все рассматриваемые здесь интегралы существуют.
1.
|
2.
|
2а.
|
2б.
;
|
3.
|
3а.
|
3б.
; ; |
4.
|
4а.
|
5.
|
5a.
|
6.
|
6a.
|
7.
|
7a.
|
8.
|
9.
|
10.
|
11.
[ |
12.
[ ] ; ; |
13.
|
14.
|
15.
|
16.
|
17.
|
;
,
;
,
;
,
;
;
,
[
];
,
[
];
,
[
];
,
,
;
,
,
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
,
[
]
;
;
,
[
]
;
;
,
[
];
,
]
;
;
,
;
,
[
];
;
;
,
[
];
,
[
].
1.4. Некоторые примеры на применение свойств и вычисления определенного интеграла
Пример 1.
Сравнить
интегралы
и
.
Решение.
Так как функция
для любого х,
то, по свойствам 6 и 7, будем иметь:
.
Пример 2. Какой из интегралов больше
или
?
Решение.
Обратим внимание на то, что подынтегральная
функция у обоих интегралов одна и та
же:
.
Причем, эта функция
− нечетная, т.к.
.
Воспользуемся
свойством 6 для второго интеграла:
,
т.к. по свойству 14
.
Следовательно,
.
Пример 3.
Сравнить
интегралы
и
.
Решение.
Функция
[
],
и, следовательно, по свойству 7, оба
интеграла будут отрицательными. Из двух
отрицательных чисел больше то, абсолютная
величина которого меньше. Следовательно,
больше тот интеграл, у которого меньше
промежуток интегрирования:
.
Пример 4.
Сравнить
интегралы
и
.
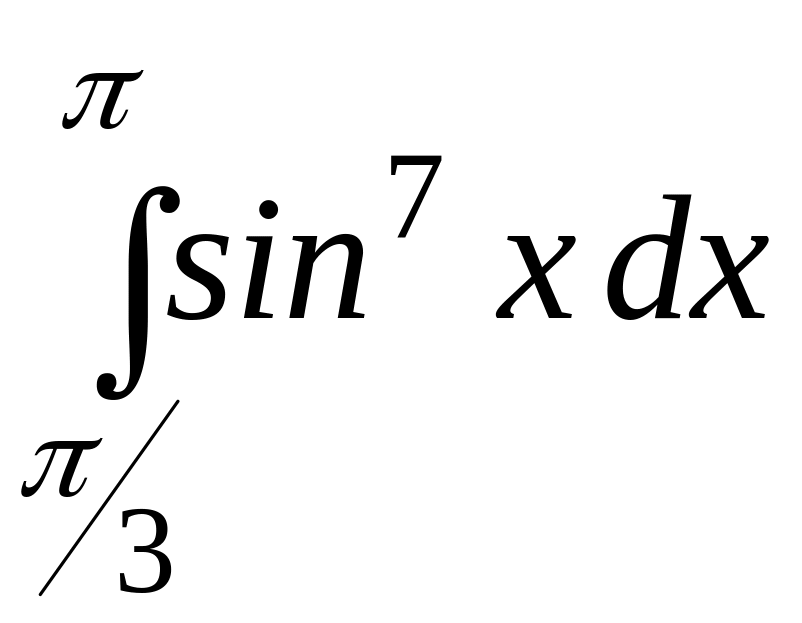Решение.
По свойству
6 имеем:
,
(
<4).
Интеграл
,
т.к.
[
],
а интеграл
,
т.к.
[
],
следовательно,
.
Пример
5. Вычислить
.
Решение. По формуле 2 из таблицы 3 имеем:
.
Пример
6. Вычислить
.
Решение.
Преобразуем подкоренное выражение,
воспользовавшись тригонометрической
формулой
:
.
Поскольку
,
а
на промежутке [
]
и
на промежутке [
],
то
.
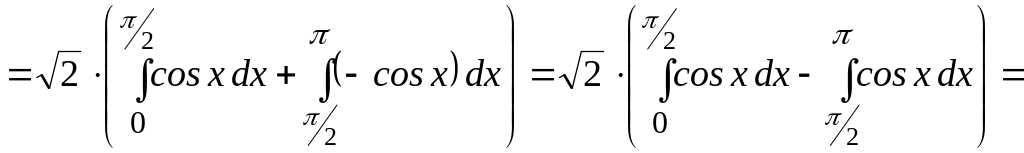
Пример
7. Вычислить
.
Решение. По свойству 3 представим данный интеграл, как сумму двух интегралов:
.
Подынтегральная функция первого интеграла является функцией нечетной, так как
.
Поэтому по свойству 14
.
Под знаком второго
интеграла стоит четная функция
,
следовательно
.
Окончательно получаем:
.