
- •1) Тпс её составные части. История развития
- •3) Функциональная схема системы связи
- •2) Сообщение сигнал, система связи, канал связи
- •4)Характеристики дискретных каналов и сигналов.
- •6) Количественное определение информации. Энтропия и производительность дискретного источника сообщения
- •7) Помехи и искажения
- •8. Сигналы и их спектры (Спектральный анализ сигналов).
- •11) Спектральный метод исследования прохождения сигналов через линейные цепи.
- •13,Модулированные колебания. Амплитудная модуляция.
- •16. Помехоустойчивость системы связи. Оптимальный фильтр.
- •17. Оптимальная фильтрация сигнала заданной формы. Передаточная функция фильтра
- •18. Физическая интерпретация частотного коэффициента передачи оптимального фильтра.
- •19) Согласованный фильтр для прямоугольного видеоимпульса с длительностью u и τ
- •20) Квазиоптимальные фильтры
- •21) Теорема Котельникова
- •26) Взаимные помехи при разделении каналов
- •27) Дискретизация и кодирование непрерывного сообщения.
- •28) Статистические свойства случайных процессов
- •30) Энергетические спектры сигналов
- •31)Корреляционные характеристики детерминированных сигналов
- •32) Связь между энергетическим спектром сигнала и его автокорреляционной функцией.
- •33)Принцип определения взаимной функции корреляции
- •34) Обработка непрерывных и дискретных сигналов
30) Энергетические спектры сигналов
Рассмотрим частотный
аспект и найдем связь между скалярным
произведением сигналов и их спектральными
плотностями. Пусть имеются два сигнала
u(t)
и V(t).
Их скалярное произведение (u,v)=![]() пропорционально взаимной энергии
сигналов и , если сигналы совпадают,
т.е. u(t)
= v(t),
то скалярное произведение переходит в
энергию сигнала:
пропорционально взаимной энергии
сигналов и , если сигналы совпадают,
т.е. u(t)
= v(t),
то скалярное произведение переходит в
энергию сигнала:
![]() .
Каждому из сигналов u(t)
и v(t)
соответствуют спектральные плотности
.
Каждому из сигналов u(t)
и v(t)
соответствуют спектральные плотности
![]() которые связаны с сигналами обратным
преобразованием Фурье
которые связаны с сигналами обратным
преобразованием Фурье
![]()
![]()
Заменим в скалярном
произведении один из сигналов его
спектральным представлением
![]() а затем сменим порядок интегрирования
по времени и частоте:
а затем сменим порядок интегрирования
по времени и частоте:![]() Внутренний интеграл есть не что иное,
как спектральная плотность сигнала
u(t)
при отрицательном значении аргумента
(т.е. частоты):
Внутренний интеграл есть не что иное,
как спектральная плотность сигнала
u(t)
при отрицательном значении аргумента
(т.е. частоты):![]() Следовательно
Следовательно
![]() .
(1) Эта запись называется обобщенной
формулой Рэлея.
.
(1) Эта запись называется обобщенной
формулой Рэлея.
Скалярное произведение двух сигналов пропорционально скалярному произведению их спектральных плотностей.( ! )
Если u(t) = v(t), то из (1) получим так называемое равенство Парсеваля:
![]() (2)
(2)
Равенство
Парсеваля устанавливает связь между
энергией сигнала и модулем его спектральной
плотности. Величина
![]() имеет смысл плотности распределения
энергии по оси частот и называется
энергетическим спектром сигнала или
спектральной плотностью энергии сигнала.
имеет смысл плотности распределения
энергии по оси частот и называется
энергетическим спектром сигнала или
спектральной плотностью энергии сигнала.
![]() (3)
(3)
т.е. энергия сигнала может быть представлена как результат суммирования вкладов в энергию от различных участков на частотной оси.
Аналогично
определяется и взаимный энергетический
спектр сигналов u(t)
и v(t):
(u,v)=![]() (4)
(4)
Вид кривой взаимного энергетического сигнала спектра Wu,v(ω) показывает, какую роль в формировании взаимной энергии сигналов (их взаимного влияния) играют различные участки их спектра. При изучении сигналов с помощью энергетических спектров неизбежно теряется информация, которая заключена в фазовых спектрах, тем не менее понятие энергетического спектра весьма плодотворно с точки зрения установления реальной ширины спектра тех или иных сигналов.
Рассмотрим распределение энергии в спектре одиночного прямоугольного видеоимпульса. Аналитическое выражение для энергетического спектра можно получить, возводя в квадрат выражение для спектральной плотности прямоугольного видеоимпульса
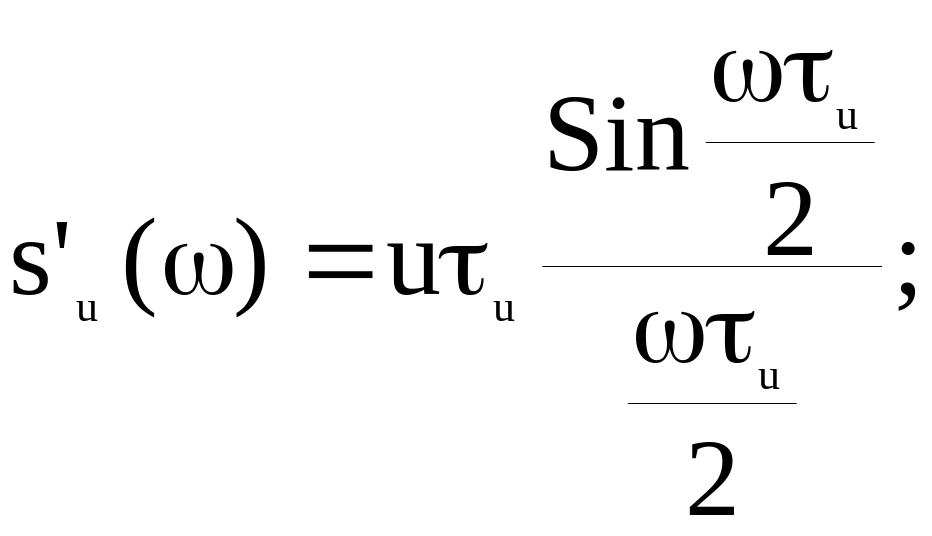
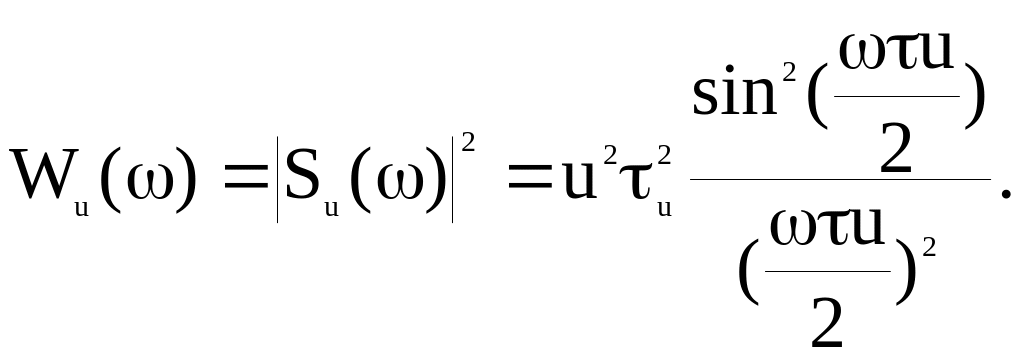 (5)
(5)
Полная
энергия такого видеоимпульса равна
![]() где U-
амплитуда импульса, τu
- длительность.
где U-
амплитуда импульса, τu
- длительность.
Рисунок
Для определения доли энергии в пределах 1-го, 2-го, 3-го лепестков спектра надо проинтегрировать (5) в соответствующих пределах. Доля энергии в 1-ом лепестке
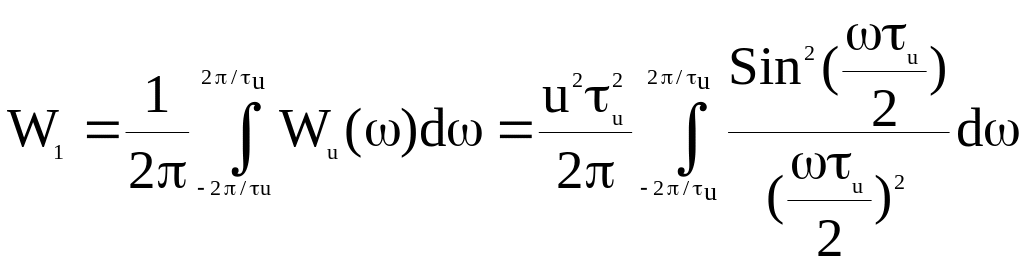
Сделаем
замену переменных
![]() тогда
тогда
![]() .
Имеется табличный интеграл
.
Имеется табличный интеграл
![]() однако в пределах от 0 до π этот интеграл
не затабулирован. Численные расчеты
показывают, что в пределах 1-го лепестка
содержится 0,902 энергии сигнала, во 2-ом
- 0,048, в 3-ьем - 0,023. Таким образом, 2-х краткое
расширение полосы пропускания приемника
увеличит энергию сигнала всего на 4,8%,
в то время. как помеха, если она имеет
равномерный спектр, увеличит свою
энергию на 100 %. На практике принято за
активную ширину спектра сигнала ΔF
принимать диапазон частот, внутри
которого сосредоточено 90 - 95% энергии
сигнала. Для прямоугольного видеоимпульса
это один-два первых лепестка.
однако в пределах от 0 до π этот интеграл
не затабулирован. Численные расчеты
показывают, что в пределах 1-го лепестка
содержится 0,902 энергии сигнала, во 2-ом
- 0,048, в 3-ьем - 0,023. Таким образом, 2-х краткое
расширение полосы пропускания приемника
увеличит энергию сигнала всего на 4,8%,
в то время. как помеха, если она имеет
равномерный спектр, увеличит свою
энергию на 100 %. На практике принято за
активную ширину спектра сигнала ΔF
принимать диапазон частот, внутри
которого сосредоточено 90 - 95% энергии
сигнала. Для прямоугольного видеоимпульса
это один-два первых лепестка.
