
- •1 Матрицы, операции над матрицами. Ранг матрицы. Обратная матрица
- •2 Системы линейных уравнений . Методы решении
- •3 Основная задача лп каноническая форма. Примеры
- •4 Симметричная форма. Примеры
- •5 Геометрическая интерпретация и графическое решение злп
- •6 Общая идея симплекс метода . Построение начального опорного плана.
- •3. Симплексный метод
- •8 Свойства решений злп.
- •9 Двойственность в лп. Пример построения двойственной задачи.
- •10 Симметричные двойственные задачи (кривая составления)
4 Симметричная форма. Примеры
Стандартной (или симметричной} задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (9) и (11), где k = m и l = n.
![]()
Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной записи имеют вид:
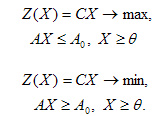
5 Геометрическая интерпретация и графическое решение злп
Задачу линейного программирования можно решить графическим методом, если
1)задача записана в симметричной форме и число переменных не превышает двух
2)задача записана в канонической форме и число свободных переменных не превышает двух (задача сводится к сл. 1)
3)задача общего вида , которая после приведения к канонической форме будет содержать не более двух свободных переменных.
Из геометрической интерпретации элементов злп следует алгоритм решения задач графическим методом:
1)строим область допустимых решений Ω
2) строим вектор с=(с1,с2)
3) строим произвольную линию уравнения Z=Z0
4) при рении задач на максим перемещаем линию уровня Z=Z0 в направлении вектора с до тех пор пока она имеет общие точки с областью Ω те находим крайнее положение в котором линия уровня кажется области допуст значен . в случае решения задач на мин линию уровня перемещают в направлении вектора(-С)
5 ) определяем оптимальный план Х*=(Х81,Х82) и экстремальное значение целевой функции Z*=Z*(Х*)
6 Общая идея симплекс метода . Построение начального опорного плана.
3. Симплексный метод
Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП состоит в следующем:
умение находить начальный опорный план;
наличие признака оптимальности опорного плана;
умение переходить к нехудшему опорному плану.
Суть симплекс-метода в том, что происходит замена одной переменной в базисе так, чтобы значение целевой функции возрастало. Поэтому в качестве переменной для ввода в базис выбирается та из yS, которой соответствует наибольшее положительное значение симплекс-разности.
8 Свойства решений злп.
В линейном программировании изучаются свойства решений линейных систем уравнений и неравенств с n-переменными следующего вида:

В системах ( коэффициенты aij и правые части bi являются числами.
Системы называются системами ограничений.
Точка в n - мерном пространстве
![]()
удовлетворяющая системе (1.1), называется допустимым планом.
Основной задачей линейного программирования (ОЗЛП) с n-переменными называется задача о нахождении такого допустимого плана, который доставляет максимум функции
![]()
Функция Z, определенная соотношением (1.3), называется функцией прибыли (целевой функцией).
Допустимый план, доставляющий максимум функции (1.3), называется оптимальным планом.
Иногда в задачах линейного программирования вместо нахождения максимума функции прибыли Z требуется найти минимум функции затрат
![]()
В этом случае с помощью введения функции Z = − R задача о нахождении минимума функции затрат R сводится к задаче о нахождении максимума функции прибыли Z.
