Практическая работа №1

Задание: Определить равномерность поставок в течение года.

1. Определить объем поставок по варианту:

П_i = П_0i + 50/N,

где П_0i – данные из таблицы, соответствующие поставкам в i-том месяце;

П_i – расчетные данные по поставкам в i-том месяце по варианту;

N – номер варианта (№ в списке группы).

Примечание. Результаты расчетов округлить до целого числа.

Таблица исходных данных:

№ месяца	1	2	3	4	5	6	7	8	9	10	11	12
Объем поставок	150	145	160	170	160	200	186	220	185	195	230	240

2. Равномерность поставок вычислить по формуле:

,

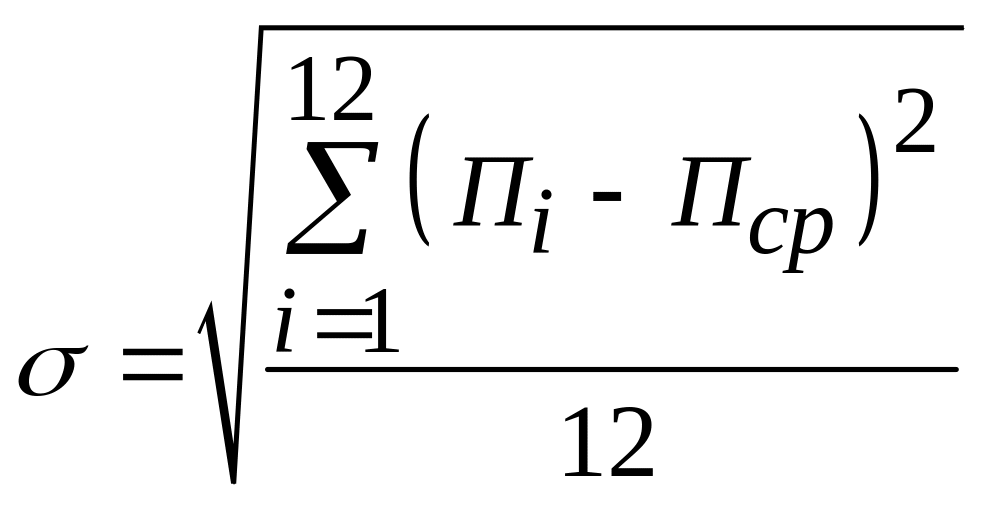где П_ср – среднее за все 12 месяцев;

П_i – соответствует поставкам в i-том месяце.

3. Вычислить дисперсию ².

4. Определить коэффициент вариации:

.

5. Рассчитать коэффициент равномерности:

.

6. Сделать вывод о равномерности поставок:

- если  = 1 – поставки абсолютно равномерны;

- если   1, то равномерность поставок нормальная;

- если   0,75, то поставки неравномерны.

7. Оформить отчет.

Практическая работа №2

Задание: Используя данные практической работы №1, оценить равномерность поставок, проведя сглаживание методом скользящих средних. Суть метода заключается в замене фактического среднего значениями суммы соседних трёх точек.

1. Сглаживание производится по следующим формулам:

, для i = 1;

, для 1 < i < n-1;

, для i = n,

где n = 12 – количество месяцев.

Результаты расчетов округлить до целого.

2. Объем поставок до и после сглаживания представить в табличной форме.

3. Для новых расчетных данных по поставкам вычислить равномерность поставок:

,

где П_ср – среднее за все 12 месяцев;

П_i – соответствует поставкам в i-том месяце.

3. Вычислить дисперсию ².

4. Определить коэффициент вариации:

.

5. Рассчитать коэффициент равномерности:

.

6. Используя расчетные данные практической работы №1, сделать вывод об изменении равномерности поставок до и после сглаживания.

7. Построить два графика по поставкам в течение года до и после сглаживания.

8. Оформить отчет.

Практическая работа №3

Задание: Используя данные практической работы №1, провести выравнивание поставок и построить многочлен кривой методом наименьших квадратов.

1. Пусть функция y = f(x) задана таблицей своих значений (см. практическую работу №1): y_i = f(x_i), i = 1,…,n. Требуется найти многочлен фиксированной степени m (примем равной 2), для которого среднее квадратическое отклонение (СКО) минимально:

,

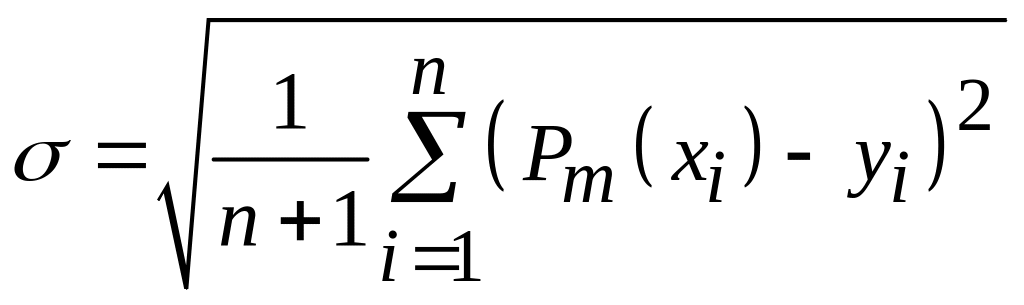где x – номер месяца;

y – объем поставок;

n = 12 – количество месяцев.

2. Решив систему уравнений любым известным Вам методом

,

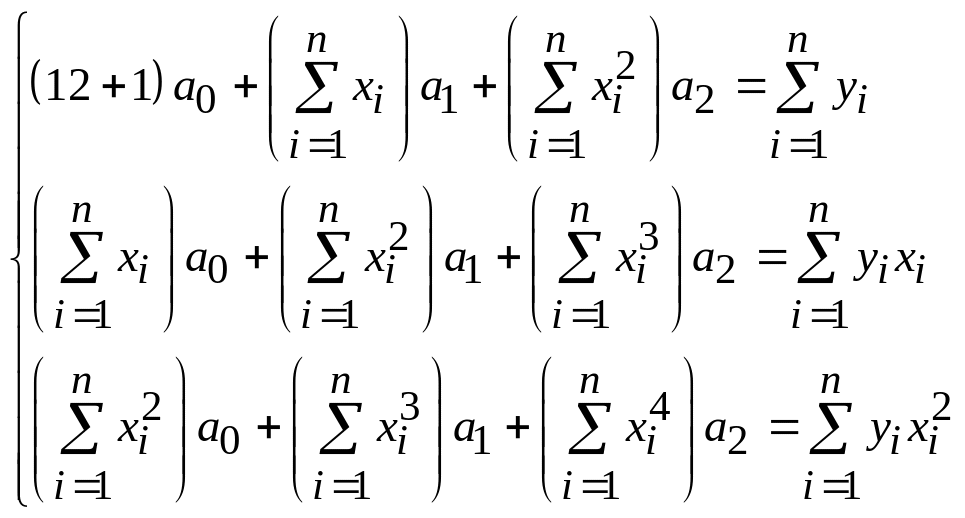получить значения коэффициентов a₀, a₁, a₂.

3. По полученным коэффициентам определить многочлен:

.

4. Найти значения многочлена для каждого конкретного x_i. Результаты вычислений представить в виде таблицы:

a0	a1xi	a2xi2	Pm(xi)

5. Построить два графика по поставкам в течение года до (практическая работа №2 (часть 1)) и после выравнивания P_m(x_i), используя данные таблицы п. 4.

6. Определить среднее квадратическое отклонение (СКО) по формуле п.1.