
- •5.Влияние напряженности магнитного поля на величину магнитной индукции ферромагнетиков.
- •11.Влияние температуры на диэлектрическую проницаемость материалов с различными механизмами поляризации.
- •23. Магнитомягкие ферриты.
- •29. Определение индексов плоскостей и направлений в кристаллах
- •35.Потери в магнитомягких материалах в переменных полях. Методы снижения потерь.
- •41.Принципы получения материалов с высокой коэрцитивной силой
- •47. Пьезоэлектрики
- •53. Электрический пробой диэлектриков
29. Определение индексов плоскостей и направлений в кристаллах
При обозначении узлов и направлений в кристаллической решетке координаты любого узла решетки можно выразить как x=ma, y=nb, z=pc, где a, b, c - параметры решетки, m, n, p - целые или дробные числа. Если за единицы измерения длин принять параметры решетки, то координатами узла будут просто целые или дробные числа m, n, p. Эти числа называют индексами узла и записывают следующим образом: (mnp) (рис. 1.8, а).
Для описания направления в кристалле выбирается прямая, проходящая через начало координат. Ее направление однозначно определяется индексами (mnp) первого узла, через который она проходит (рис. 1.8, а). Поэтому индексы узла одновременно являются и индексами направления. Индексы направления обозначаются так: [mnp]. Строго говоря, указанные индексы определяют целое семейство физически эквивалентных направлений в кристалле, получаемых циклической перестановкой значений индексов m, n, p. Индексы эквивалентных направлений обозначаются <mnp>. Отметим, что если в символах узлов могут применяться дробные индексы, то для символов направлений и плоскостей используются только целочисленные индексы.
Д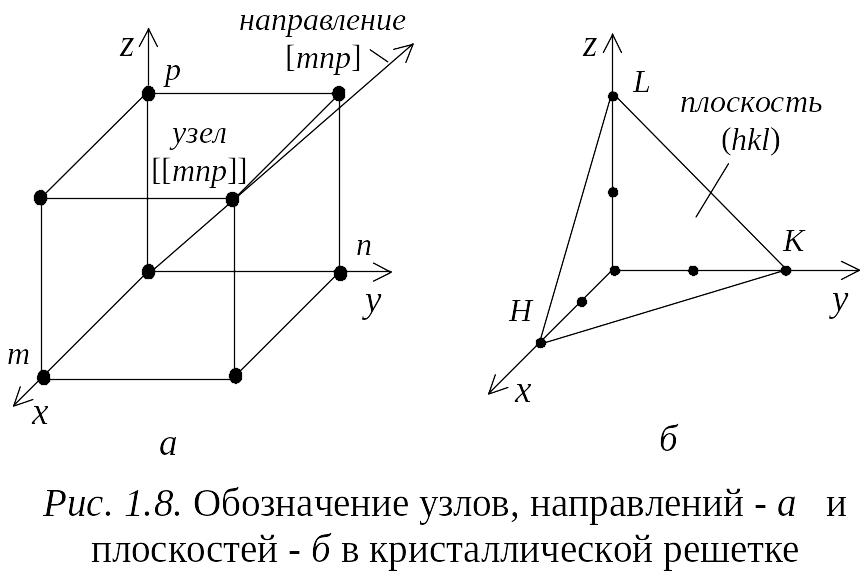 ля
обозначения индексов
плоскостей используются
индексы Миллера, которые
находятся следующим образом: выражают
отрезки H,
K, L,
которые плоскость отсекает на осях
решетки (рис. 1.8, б),
в осевых единицах H=m,
K=n, L=p,
где m,
n, p
- целые числа (координаты узлов),
не равные нулю. Записывают величины,
обратные этим отрезкам, 1/m,
1/n, 1/p.
Находят наименьшее целое
общее кратное (НОК) чисел m,
n, p.
Пусть НОК=d.
В этом случае индексами Миллера
плоскости будут являться целые
числа h=d/m,
k=d/n, l=d/p,
которые записываются так: (hkl).
ля
обозначения индексов
плоскостей используются
индексы Миллера, которые
находятся следующим образом: выражают
отрезки H,
K, L,
которые плоскость отсекает на осях
решетки (рис. 1.8, б),
в осевых единицах H=m,
K=n, L=p,
где m,
n, p
- целые числа (координаты узлов),
не равные нулю. Записывают величины,
обратные этим отрезкам, 1/m,
1/n, 1/p.
Находят наименьшее целое
общее кратное (НОК) чисел m,
n, p.
Пусть НОК=d.
В этом случае индексами Миллера
плоскости будут являться целые
числа h=d/m,
k=d/n, l=d/p,
которые записываются так: (hkl).
Например,
пусть для некоторой плоскости
m=1,
n=4,
p=2.
Тогда d=4
и, следовательно, индексы
Миллера этой плоскости равны: h=4,
k=1,
l=2,
то есть (hkl)=(412).
Индексы Миллера для значений
m,
n
или р,
равных бесконечности (случай,
когда плоскость параллельна
одной или двум осям координат),
принимаются равными нулю.
Например, для значений m=3,
n=![]() ,
p=
индексы Миллера данной
плоскости равны (100).
,
p=
индексы Миллера данной
плоскости равны (100).
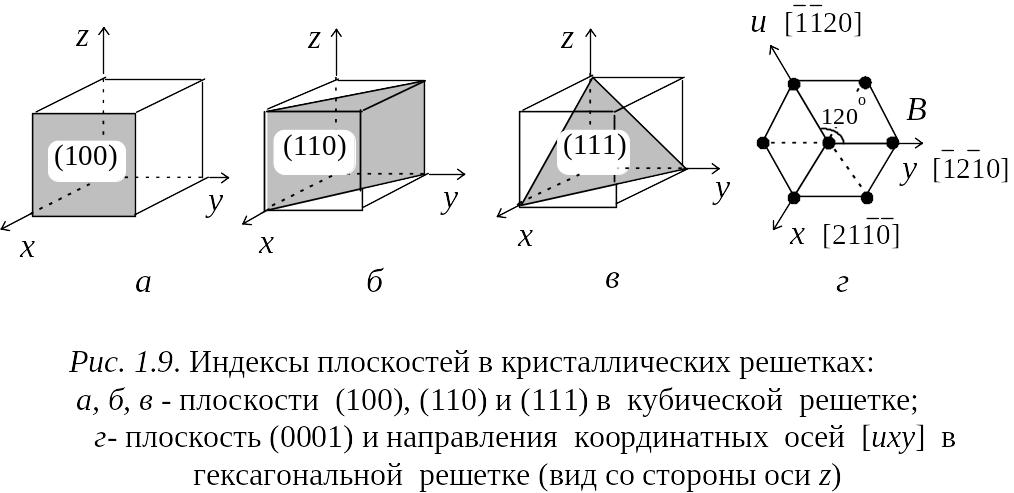
Так же, как и индексы направлений, индексы Миллера определяют не одну плоскость, а целое семейство плоскостей. Совокупность физически эквивалентных плоскостей, например всех шести граней куба, обозначают {hkl}. В качестве примера на рис. 1.9 приведены обозначения основных плоскостей и направлений в кубической и гексагональной решетках. В кубической решетке (рис. 1.9, а- в) индексы плоскости совпадают с индексами направления, перпендикулярного этой плоскости.
Правила.
1)выбрать систему отсчета(любой произвольный атом в кристаллической решетке)
2)оси по возможности располагают перпендикулярно друг другу и располагают их так, чтобы расстояние между атомами были минимальным
3) за единицу отсчета – расстояние между атомами
Чтобы найти направление, из начала отсчета проводят вектор параллельный направлению и записывают координаты угла, которого досигнет этот вектор.
