
- •Вопрос 2
- •Вопрос 3.
- •Вопрос 5.
- •Вопрос 6.
- •Вопрос 7.
- •Вопрос 8.
- •Вопрос 9.
- •Вопрос 10.
- •Вопрос 11.
- •Вопрос 12.
- •Вопрос 13.Большее значение функции) рвале, если доя любых точек х
- •Вопрос 14.
- •Вопрос 15.
- •Вопрос 16.
- •Вопрос 17.
- •Вопрос 18
- •Вопрос 19.
- •Вопрос 20.
- •Вопрос 21.
- •Вопрос 22.
- •Вопрос 23.
- •Вопрос 24.
- •Вопрос 25.
- •Вопрос 26.
- •Вопрос 27.
- •Вопрос 28.
- •Вопрос 29.
- •Вопрос 30. Несобственный интеграл по неограниченному промежутку.
Математика. Экзамен
Вопрос 2
Числовая последовательность.
Если каждому натуральному числу n сопоставлено действительное число хn, то множество чисел х1,х2…хn, называется последовательностью.
Предел последовательности.
Число а называется пределом числовой последовательности, если для любого положительного и сколько угодно малого числа Е существует номер N, начиная с которого все элементы последовательности будут находиться на расстоянии от точки a меньше, чем от Е.
Число а называется приделом последовательности, если для любого положительного и сколь угодно малого числа Е найдется номер N, начиная с которого все элементы последовательности удовлетворяют неравенству | xn-a|<E.
Примеры.
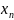 =
1 -1/n
=
1 -1/n
Вопрос 3.
Предел функции.
Число А называется пределом функции f(x) при х стремящийся к а, если для любой последовательности {xn}такой, что предел стремящийся к бесконечности xn=а, соответствующая последовательность значений функции f(x1), f(x2), f(x3), . . . . f(xN), имеет предел, равный одному и тому же числу А.
Обозначение:
![]() (у
нас равно А)
(у
нас равно А)
Свойства пределов.
Вопрос 5.
Первый и второй замечательные пределы.
1)

2)
![]()
(Дописать)
Вопрос 6.
Непрерывность функций в точке.
Пусть функция y=f(x) определена на некотором интервале (a;b), содержащем точку х0. Функция называется непрерывной в точке х0, если существует конечный предел при Х→Х0 и он равен значению функции в этой точке.
![]()
![]()
Если функция непрерывна в любой точке интервала (a;b), то она называется непрерывной на этом интервале.
Точка разрыва.
Если в некоторой точке функция не является непрерывной, то эта точка называется точкой разрыва функции.
Примеры.
Функция f(x)
= ![]() имеет
в точке х0 =
0 точку разрыва т.к.
имеет
в точке х0 =
0 точку разрыва т.к.
![]() .
.
Вопрос 7.
Функции, непрерывные на интервале.
Определение.
Функция y=f(x) называется непрерывной на интервале (a;b), если она непрерывна в любой точке этого интервала.
Утверждение.
Если функция f(x) непрерывна на интервале (a;b), то функция с*f(x) непрерывна на (a;b). Если функции f(x) и g(x) непрерывны на (a;b), то функции f(x)±g(x), f(x)*g(x) тоже непрерывны на (a;b), причем если g(x)≠0 при любом Х€(a;b), то функция f(x)/g(x) тоже непрерывна на интервале (a;b).
Вопрос 8.
Производная функции, ее геометрический и механический смысл.
Пусть
функция y=f(x)
определена на некотором интервале
(a;b),
содержащем точку Х0.
Если
существует конечный предел
![]() ,
то этот предел и называется производной
функции y=f(x)
в точке Х0.
,
то этот предел и называется производной
функции y=f(x)
в точке Х0.
![]()
Производная функции в точке Х0 есть предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к 0.
Геометрический смысл.
Производная функции y=f(x) в точке Х0 равна тангенсу угла наклона касательной к графику функции в этой точке.
Механический смысл.
Пусть
материальная точка движется прямолинейно
и ![]() -
длина пути, проходимого за время
-
длина пути, проходимого за время ![]() ,
отсчитываемого от некоторого момента
времени
,
отсчитываемого от некоторого момента
времени ![]() .
.
Для
определения скорости ![]() в
данный момент
придадим
переменной
некоторое
приращение
в
данный момент
придадим
переменной
некоторое
приращение ![]() ,
при этом приращение пути будет равно
,
при этом приращение пути будет равно ![]() .
.
Отношение ![]() называется
в физике величиной средней скорости
движения за промежуток времени, начиная
с момента времени
,
и обозначается
называется
в физике величиной средней скорости
движения за промежуток времени, начиная
с момента времени
,
и обозначается
![]()
Предел ![]() называется
величиной мгновенной скорости движения
в момент времени
.Таким
образом, мгновенная скорость в момент
времени
прямолинейного
движения, совершаемого по закону
равна
значению производной
называется
величиной мгновенной скорости движения
в момент времени
.Таким
образом, мгновенная скорость в момент
времени
прямолинейного
движения, совершаемого по закону
равна
значению производной ![]() .
.
Уравнение касательной к графику функции y=f(x), в точке (X0; f(x0))
Yкас.= f(x0) + f `(x0)*(x-x0)
Дифференцируемость.
Если функция имеет производную в точке х0, то она называется дифференцируемой в точке х0, а нахождение её производной называется дифференцированием функции.
Утверждение. Если функция y=f(x) дифференцируема в точке х0, то она и непрерывна в этой точке.
Замечание. Из непрерывности функции в точке дифференцируемость в этой точке не следует.


