
- •Двойные интегралы.
- •2. Тройные интегралы.
- •Криволинейный интеграл первого рода.
- •2. Криволинейный интеграл второго рода.
- •Связь между криволинейным интегралом второго рода вдоль замкнутой кривой на плоскости и двойным интегралом. Формула Грина.
- •Условие независимости криволинейного интеграла второго рода от пути интегрирования на плоскости.
- •Поверхностный интеграл первого рода.
- •2. Поверхностный интеграл второго рода.
- •Связь криволинейного интеграла второго рода по замкнутой кривой в пространстве с поверхностным интегралом. Формула Стокса.
- •Условие независимости криволинейного интеграла второго рода от пути интегрирования в пространстве.
- •5. Связь интеграла по замкнутой поверхности с тройным интегралом по телу, ограниченному этой поверхностью. Формула Гаусса-Остроградского.
Связь между криволинейным интегралом второго рода вдоль замкнутой кривой на плоскости и двойным интегралом. Формула Грина.
Пусть C
– кусочно-гладкая замкнутая кривая,
ограничивающая область D.
На кривой C
задано такое направление, что при
движении в этом направлении область D
остается слева. Функции
![]() и
и
![]() непрерывны в области D
вплоть до ее границы, кроме того, функции
непрерывны в области D
вплоть до ее границы, кроме того, функции
![]() и
и
![]() также непрерывны в D
вплоть до границы. Тогда справедлива
формула Грина
также непрерывны в D
вплоть до границы. Тогда справедлива
формула Грина
![]() .
(ФГ)
.
(ФГ)
1. Докажем формулу Грина сначала для случая, когда область D выпукла в направлении координатных осей, то есть, любые прямые, параллельные осям координат и пересекающие область D, пересекают ее границу либо не более, чем в двух точках, либо по отрезку прямой.
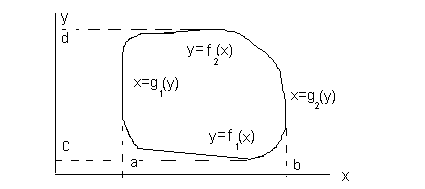
Обозначим,
как это показано на рисунке, проекции
области D
на координатные оси
и
.
Запишем уравнения фрагментов кривой
C,
однозначно проецирующихся на
,
в виде
![]() .
Запишем уравнения фрагментов кривой
C,
однозначно проецирующихся на
,
в виде
.
Запишем уравнения фрагментов кривой
C,
однозначно проецирующихся на
,
в виде
![]() .
.
Сосчитаем
сначала интеграл
![]() .
Представим его в виде суммы криволинейных
интегралов по двум фрагментам, однозначно
проецирующимся на отрезок
.
Если на C
есть еще и отрезок, параллельный оси
OY,
то рассматриваемый интеграл по этому
отрезку равен нулю, так как
.
Представим его в виде суммы криволинейных
интегралов по двум фрагментам, однозначно
проецирующимся на отрезок
.
Если на C
есть еще и отрезок, параллельный оси
OY,
то рассматриваемый интеграл по этому
отрезку равен нулю, так как
![]() .
На первом фрагменте мы получим
параметризацию
.
На первом фрагменте мы получим
параметризацию
![]() причем в соответствии с заданием
направления движения параметр
должен
возрастать, когда мы движемся по этому
фрагменту в заданном направлении. На
втором фрагменте имеем параметризацию
причем в соответствии с заданием
направления движения параметр
должен
возрастать, когда мы движемся по этому
фрагменту в заданном направлении. На
втором фрагменте имеем параметризацию
![]() причем параметр
убывает, когда мы движемся по второму
фрагменту в заданном направлении. Таким
образом,
причем параметр
убывает, когда мы движемся по второму
фрагменту в заданном направлении. Таким
образом,
![]()
![]()
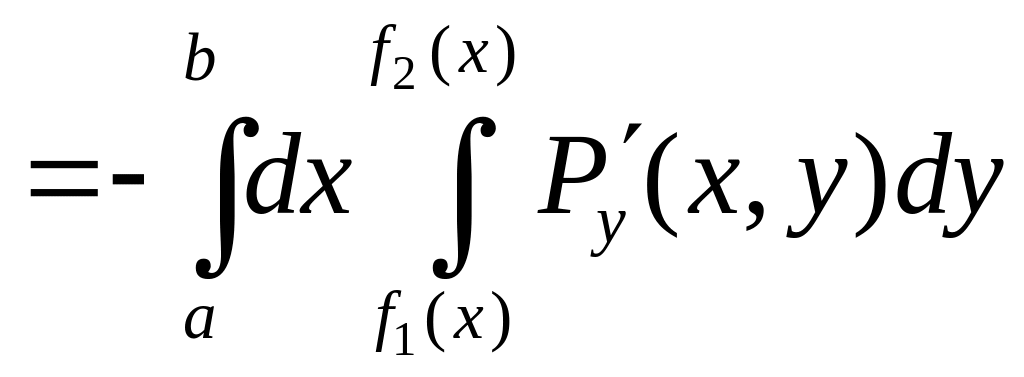
![]() .
.
Для того, чтобы
сосчитать интеграл
![]() ,
разобьем С на фрагменты, однозначно
проецирующиеся на отрезок
.
В случае, когда на C
есть отрезок, параллельный OX,
то на нем
,
разобьем С на фрагменты, однозначно
проецирующиеся на отрезок
.
В случае, когда на C
есть отрезок, параллельный OX,
то на нем
![]() ,
и значит рассматриваемый интеграл вдоль
этого отрезка обращается в ноль. На
первом фрагменте введем параметризацию
,
и значит рассматриваемый интеграл вдоль
этого отрезка обращается в ноль. На
первом фрагменте введем параметризацию
![]() причем при заданном направлении движения
параметр
должен убывать при проходе по этому
фрагменту. На втором фрагменте
параметризация
причем при заданном направлении движения
параметр
должен убывать при проходе по этому
фрагменту. На втором фрагменте
параметризация
![]() и параметр
возрастает при проходе по фрагменту в
заданном направлении. Следовательно,
и параметр
возрастает при проходе по фрагменту в
заданном направлении. Следовательно,
![]()
![]()
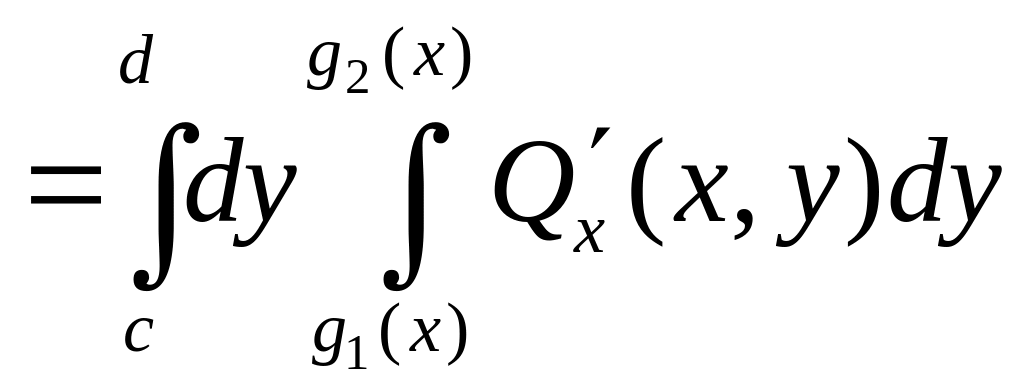
![]() .
.
Суммируя, получим формулу Грина для областей указанного вида.
2. Для доказательства
справедливости формулы Грина для области
D
общего вида разобьем область D
на конечное число областей
![]() ,
,
![]() рассмотренного выше вида проведением
прямых, параллельных осям OX
и OY.
рассмотренного выше вида проведением
прямых, параллельных осям OX
и OY.
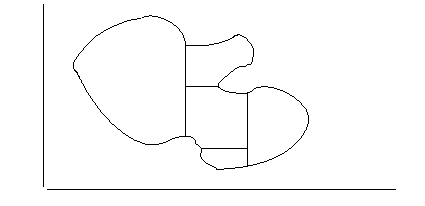
Границы полученных
таким образом областей
,
состоят из фрагментов кривой C
и из отрезков, параллельных координатным
осям. Заметим, что при последовательном
обходе границ
![]() ,
всех
полученных областей
,
так, чтобы область
находилась слева, каждый из отрезков,
параллельных координатным осям,
образовавшихся при разрезании D,
проходится дважды: в ту и в другую
стороны. Значит, при вычислении
криволинейного интеграла
,
всех
полученных областей
,
так, чтобы область
находилась слева, каждый из отрезков,
параллельных координатным осям,
образовавшихся при разрезании D,
проходится дважды: в ту и в другую
стороны. Значит, при вычислении
криволинейного интеграла
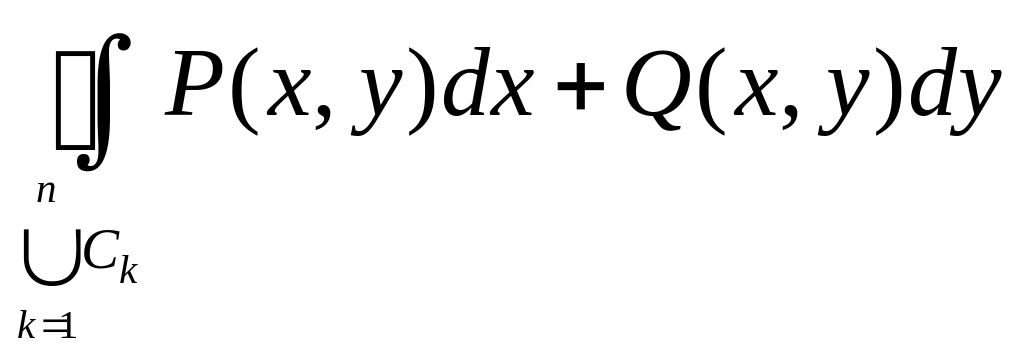 мы
получим взаимное уничтожение интегралов
вдоль прямолинейных отрезков внутри
D.
мы
получим взаимное уничтожение интегралов
вдоль прямолинейных отрезков внутри
D.
Следовательно, применяя к каждой из областей , формулу Грина, получим
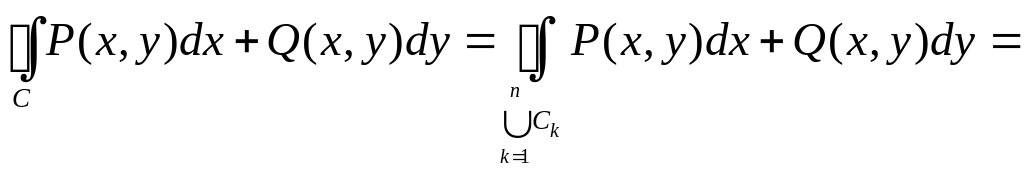
![]()
![]() .
.
