Теорема Коши

   Пусть функции f (x) и g(x) непрерывны на [a, b] и дифференцируемы на (a, b). Пусть, кроме того, во всех точках интервала (a, b) функция g(x) имеет ненулевую производную g ' (x) ≠ 0. Тогда существует точка c  (a, b), такая, что справедлива формула

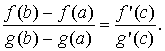
Д о к а з а т е л ь с т в о. Покажем сначала, что знаменатель левой части формулы не обращается в ноль. Если допустить, что g(b) = g(a), то по теореме Ролля для функции g(x) найдется точка   (a, b), в которой g ' () = 0. А это противоречит условию, что g ' (x) ≠ 0 на (a, b).    Рассмотрим функцию

.

Функция F(x) на [a, b] удовлетворяет условиям теоремы Ролля: F(x) непрерывна на [a, b], дифференцируема на (a, b), и, кроме того, на концах интервала принимает равные значения F(a) = F(b) = 0. По теореме Ролля для F(x) существует точка c  (a, b) , такая ,что F ' (c) = 0. Так как

,

то

.

Откуда, учитывая, что g '(c) ≠ 0, следует искомое соотношение.

17. Правило Лопиталя.

Правило Лопиталя

Будем говорить, что отношение функций f(x)/g(x) представляет собой неопределенность вида 0/0 при x a, если

lim_x af(x) = lim_x ag(x) = 0.

Раскрыть неопределенность - это значит вычислить предел lim_x af(x)/g(x), если он существует. Аналогично можно ввести понятие неопределенности при x a-0 (x a+0), x.

Следующая теорема дает правило раскрытия неопределенности вида 0/0.

Теорема 7 (правило Лопиталя). Пусть множество  (a) - проколотая  - окрестность точки a, функции f(x),g(x) определены и дифференцируемы на  , g'(x) 0,

lim_x af(x) = lim_x ag(x) = 0.

Тогда если существует lim_x af'(x)/g'(x), то существует и предел lim_x af(x)/g(x), причем справедливо соотношение

lim_x af(x)/g(x) = lim_x af'(x)/g'(x).

Данная теорема без изменений переносится на случай неопределенности вида /.

Замечание. Сформулированная теорема представляет собой лишь достаточное условие. То есть предел отношения функций может существовать и в случае, когда предел отношения производных не существует.

Например, пусть f(x) = x+sin x, g(x) = x-sin x, x. Попробуем применить правило Лопиталя

lim_x(x+sin x)/(x-sin x) = / = =lim_x(x+sin x)'/(x-sin x)' = lim_x (1+cos x)/(1-cos x),

но предел последнего выражения не существует, однако, если поделить числитель и знаменатель на x, то легко получим конечное значения предела:

lim_x(x+sin x)/(x-sin x) = lim_x (1+sin x/x)/(1-sin x/x) = 1

18. Определение производной. Её геометрический и механический смысл.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.

Пусть в некоторой окрестности точки   определена функция   Производной функции называется такое число  , что функцию в окрестности U(x₀) можно представить в виде

f(x₀ + h) = f(x₀) + Ah + o(h)

если   существует.