3*. Середнє квадратичне відхилення
Найбільш застосовною мірою розсіювання
є не дисперсія, а середнє квадратичне
відхилення. Для того, щоб мати характеристику
розсіяння, яка має розмірність однакову
з розмірністю випадкової величини і її
математичного сподівання, беруть корінь
квадратний з дисперсії зі знаком плюс.
Середнім квадратичним відхиленням
випадкової величини
називається корінь квадратний з
дисперсії, взятий зі знаком плюс, тобто
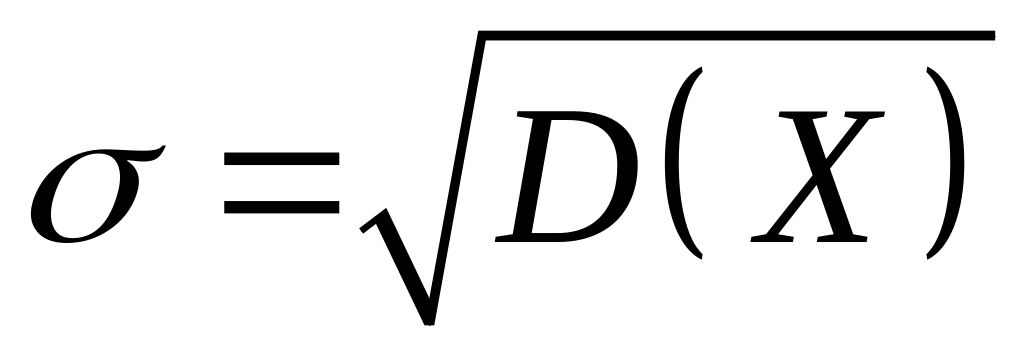 .
.
Властивості середнього квадратичного відхилення
Теорема. Середнє квадратичне
відхилення суми скінченого числа взаємно
незалежних випадкових величин дорівнює
квадратному кореню з суми квадратів
середніх квадратичних відхилень цих
величин:
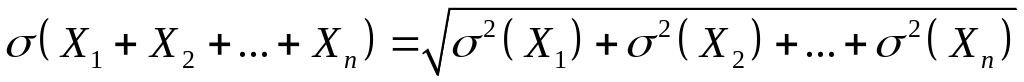 .
.
Доведення. Позначимо через
суму розглядуваних взаємно незалежних
величин:
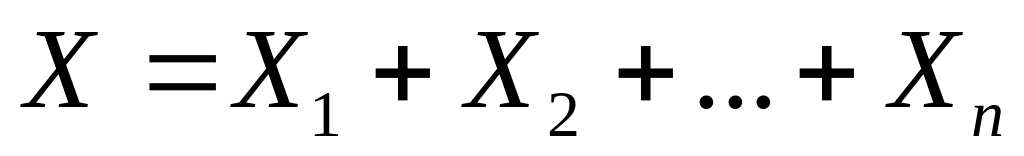 .
.
Оскільки дисперсія суми декількох
взаємно незалежних випадкових величин
дорівнює сумі дисперсій доданків, то
 ,
,
звідки
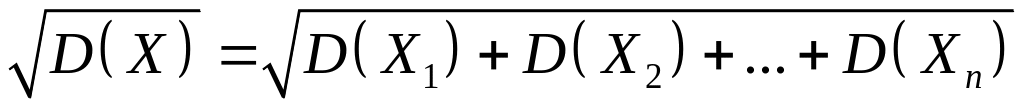 ,
або остаточно
,
або остаточно
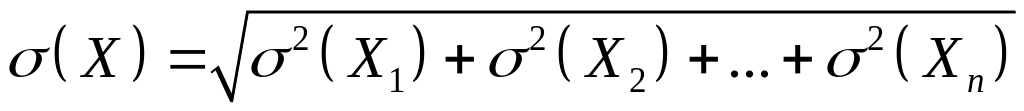 .
.
Теорема. Середнє квадратичне
відхилення середнього арифметичного
однаково розподілених взаємно незалежних
випадкових величин в
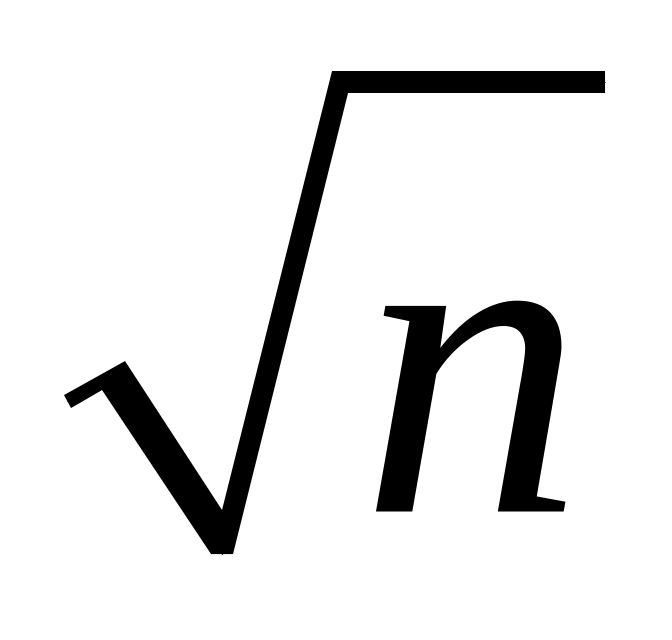 разів менше середнього квадратичного
відхилення
разів менше середнього квадратичного
відхилення
 кожної з величин:
кожної з величин:
 . (**)
. (**)
Доведення. Оскільки
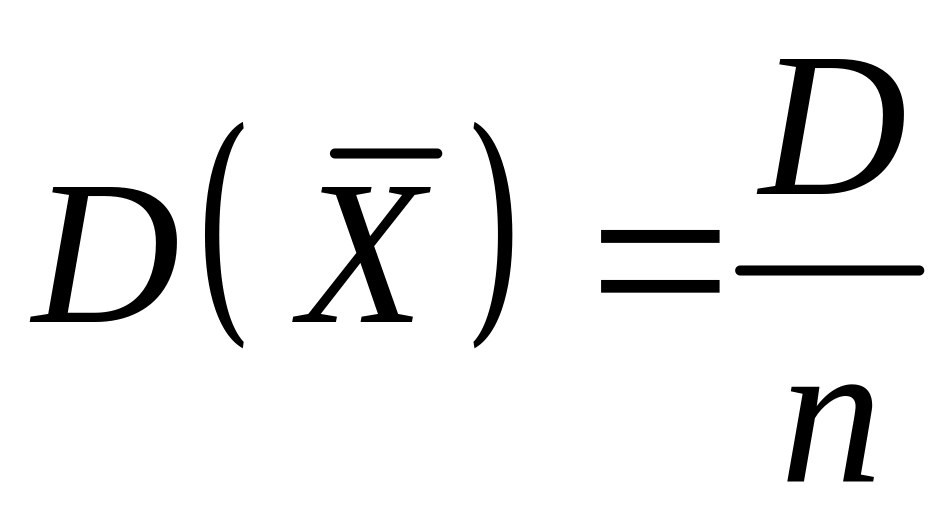 ,
то середнє квадратичне відхилення
середнього арифметичного
дорівнює
,
то середнє квадратичне відхилення
середнього арифметичного
дорівнює
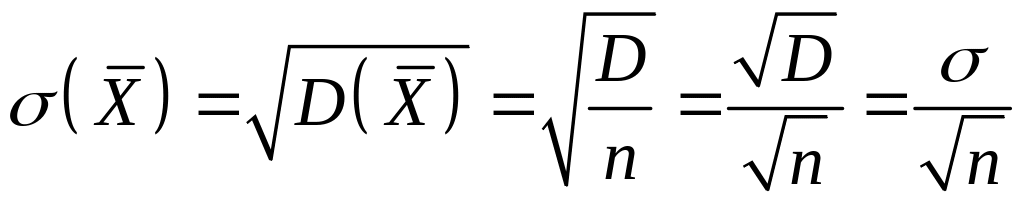 .
.
12


 . (**)
. (**)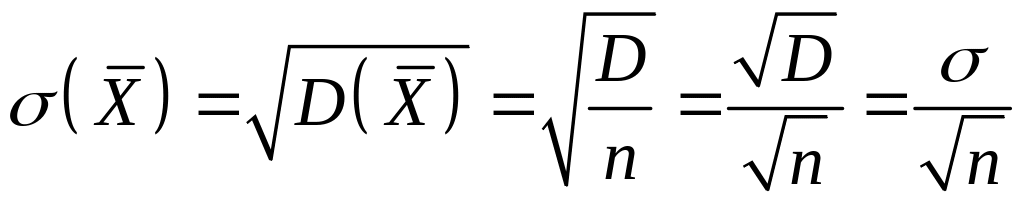 .
.