Основные этапы стеганографического преобразования

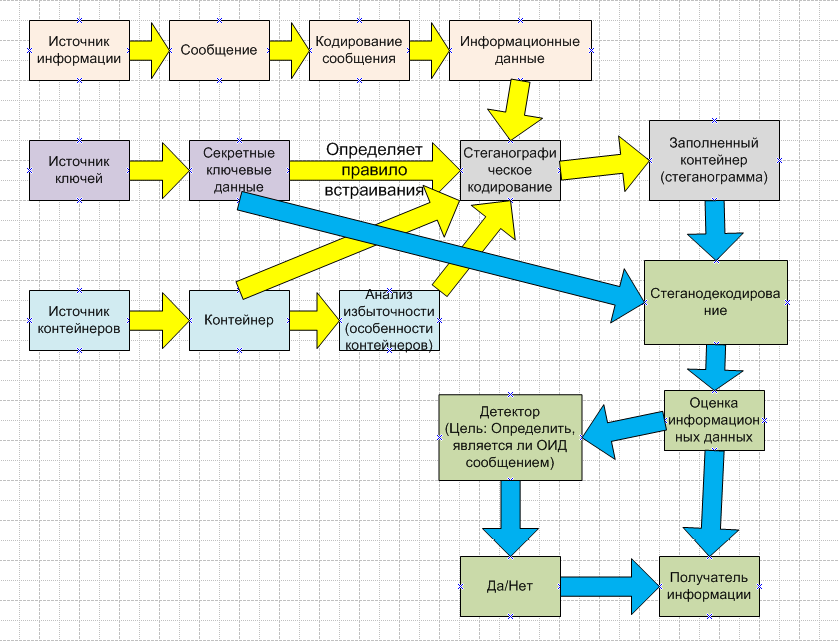
Классификация стеганосистем

Робастные стеганосистемы – это стеганосистемы устойчивые к внешним воздействиям на стеганоконтейнер. Воздействие на контейнер не приводит к разрушению или повреждению встроенного в контейнер сообщения.

Хрупкие стеганосистемы – это стеганосистемы, при которых малейшее воздействие на контейнер приводит к полному разрушению сообщения. Например, термос с очень хрупкой колбой для сохранения температуры.

Полухрупкие стеганосистемы – это стеганосистемы, которые находятся по характеристикам между робастными и хрупкими стеганосистемами. Информационное сообщение не разрушается под воздействием на контейнер до некоторой пороговой величины. После превышения этой пороговой величины информационное сообщение разрушается.

В зависимости от функционального назначения применяют одну из указанных стеганосистем:

• хрупкие, если лучше уничтожить сообщение, но не дать его в руки противнику (напр., при дипломатической переписке, военном деле, в случае со шпаргалкой).

• робастные при встраивании ЦВЗ (модификация контейнера не разрушает ЦВЗ), при защите авторского права с помощью идентификационных номеров, при встраивании заголовков (чипа).

• полухрупкие при некоторой средней ситуации.

Классификация стеганодетекторов

Стеганосистемы по виду детекторов делятся на: открытые, полузакрытые, закрытые.

В открытых стеганосистемах для детектирования информации используют в качестве входных данных только полученную оценку с выхода стеганодекодера.

В полузакрытых стеганосистемах для детектирования используют помимо полученной оценки еще и исходный ЦВЗ.

В закрытых стеганосистемах для детектирования необходимо помимо оценки с выхода декодера и исходного ЦВЗ наличие пустого контейнера.

Лекция №2 математическая модель и структурная схема стеганографической системы Математическая модель и структурная схема стеганографической системы

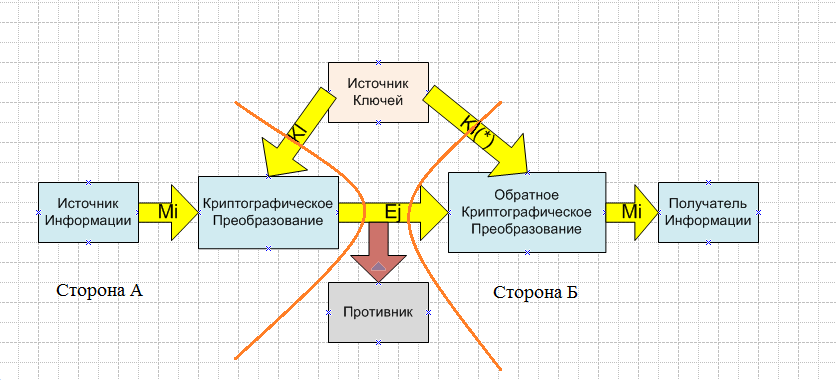
Источник информации (ИИ) формирует сообщение , принадлежащее множеству возможных сообщений . Работа ИИ описывается некоторым случайным процессом, конкретная реализация которого – суть сообщения . Следовательно, каждому на выходе ИИ можно поставить соответствующие вероятности появления их на выходе ИИ.

Пример: ИИ – подбрасывание монетки: – решка, – орел; ;

Распределение этих вероятностей характеризует производительность ИИ (количество бит информации в единицу времени).

Энтропия – производительность ИИ.

Криптографическое преобразование (КП) каждому , поступившему на его вход, ставит в соответствие некоторую криптограмму , причем  множество возможных криптограмм на выходе КП.

Таким образом, криптопреобразование реализует некоторое отображение множества открытых текстов в множество криптограмм.

Источник ключей (ИК) порождает некоторый ключ , , принадлежащий множеству возможных ключей. Работа ИК также описывается некоторым случайным процессом, конкретная реализация которого – суть ключа . Следовательно, каждому ключу припишем вероятность . Распределение этих вероятностей характеризует производительность ИК.

Ключ параметризирует (задет конкретный вид) отображения . . Таким образом, каждому введенному ключу соответствует одно из возможных отображений .

Обратное криптопреобразование (ОКП) реализует обратное отображение , параметризируемое ключом .

ПИ – получатель информации.

Противник / злоумышленник (Пр. (Зл.)) наблюдает канал связи и перехватывает .

Цели противника:

1. По известной криптограмме или некоторой их совокупности восстановить информационное сообщение , т.е. 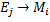(без знания секретного ключа) – задача без ключевого чтения.

2. Найти секретный ключ расшифрования , т.е. .

При решении первой задачи (Пр. (Зл.)) пытается сформировать множество апостериорных вероятностей :

, , …, .

Для второй задачи: множество апостериорных вероятностей

, , … , .

Если сформированные (Пр. (Зл.)) апостериорные вероятности равны апостериорным вероятностям при сколько угодно много перехваченных , такая секретная система называется теоретически недешифруемой (совершенно стойкой / безусловной стойкости).

Это условие соответствует простому угадыванию противником переданной информации .

Необходимое условие реализации теоретически недешифруемых систем:

1. секретный ключ формируется случайно, равновероятно и независимо от других ключей;

2. мощность множества секретных ключей больше или равна множества информационных сообщений: .

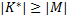Эти условия реализуются в так называемом одноразовом ключевом блокноте (шифр Вернама).

Пример реализации подобной криптосистемы изображен следующим образом:

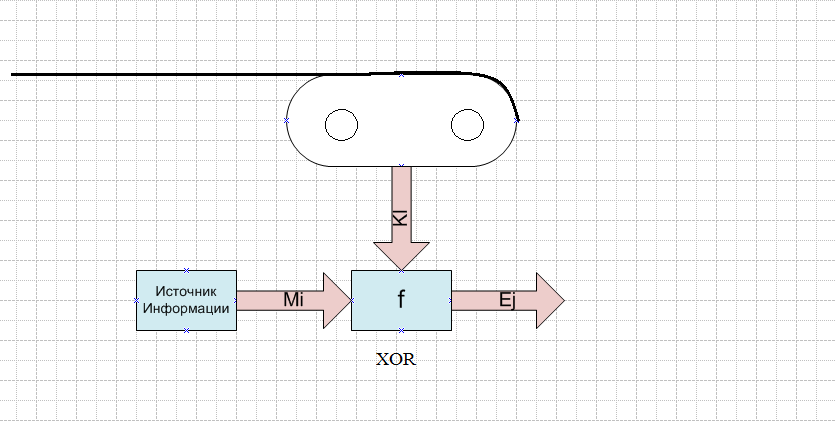
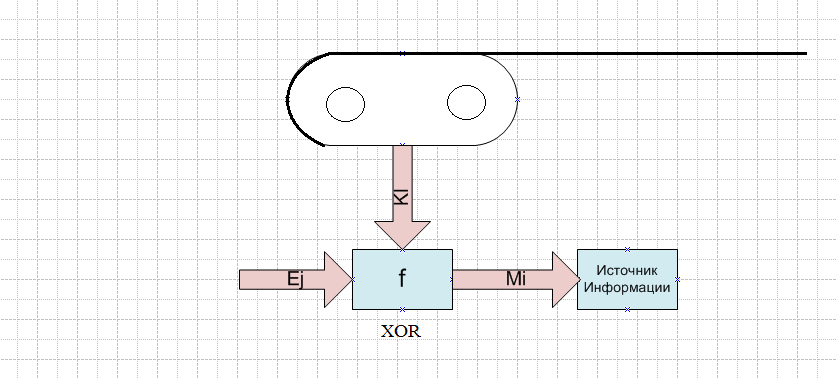
Пусть имеется лента бесконечной длины, на которую нанесены символы секретного ключа, которые сформированы случайно, равновероятно и независимо друг от друга.

Пусть имеется ИИ – источник информации, который формирует .

ИИ формирует отдельный символ сообщения, который преобразуется некоторой функцией f с очередным символом K_l , считанным со случайной ленты.

Например, на ленте записана случайная последовательность «0» и «1». ИИ формирует двоичное сообщение, каждый бит информации может ксориться с очередным битом ключа K_l: .

Теоретически недешифруемую систему можно реализовать лишь с некоторыми допущениями, т.е. приняв за истину предположение о бесконечности случайно, равновероятно и независимо сформированной последовательности символов ключа.