67. Уравнение Мещерского
— основное уравнение в механике тел переменной массы, полученное Иваном Мещерским в 1904 году. Оно имеет вид:
,
где:
m — переменная масса тела;
v — скорость движения тела переменной массы;
F — внешние силы (сопротивление среды и т. п.);
—
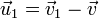относительная
скорость отделяющихся частиц;
—
относительная
скорость присоединяющихся частиц;
—
секундный
расход массы;
—
секундный
приход массы.
Реактивная тяга — сила, возникающая в результате взаимодействия двигательной установки с истекающей из сопла камеры сгорания струей расширяющихся продуктов сгорания, обладающих кинетической энергией.[1]
Природа возникновения реактивной тяги заключена в физико-химических процессах протекающих в двигательной установке при сгорании топлива. Реактивная тяга обычно рассматривается как сила реакции отделяющихся частиц. Точкой приложения её считают центр истечения - центр среза сопла двигателя, а направление - противоположноевектору скорости истечения продуктов сгорания (или рабочего тела, в случае не химического двигателя) . То есть, реактивная тяга:
приложена непосредственно к корпусу реактивного двигателя;
обеспечивает передвижение ракетного двигателя и связанного с ним аппарата в сторону, противоположную направлению реактивной струи.[2]
68. Формула при отсутствии внешних сил
Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.
,
где
— масса ракеты
—
её ускорение
— скорость истечения
газов
—
расход
массы топлива в
единицу времени
Поскольку скорость истечения продуктов сгорания (рабочего тела) определяется физико-химическими свойствами компонентов топлива и конструктивными особенностями двигателя являясь постоянной величиной при не очень больших изменениях режима работы реактивного двигателя, то величина реактивной силы определяется в основноммассовым секундным расходом топлива.[1]
69. Формула Циолковского
Основная статья: Формула Циолковского
Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского[4]:
Релятивистское обобщение этой формулы имеет вид:
,
где 
— скорость
света.