6. Среднеквадратичное (действующее) значение синусоидального тока.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

P>Если в цепь переменного синусоидального тока включить прибор, который предназначен для измерения среднего значения тока, в цепи, то этот прибор зафиксирует нулевое значение. Действительно, в каждый период ток протекает полпериода в одном направлении и полпериода – в другом.

Действующее (эффективное) значение переменного тока численно равно эквивалентной по тепловому действию силе постоянного тока, то есть такому току, который за то же время, на том де сопротивлении выделит такое же количество тепла, что и переменный ток одинаковой силы.

В цепи постоянного тока на сопротивлении R за время Т при силе тока I выделяется количество теплоты

Q=I²RT (1)

В подобном сопротивлении, включенном в цепь переменного тока, в каждый очень короткий отрезок времени ∆ t , в течение которого мгновенно значение силы тока i можно считать практически неизменным, выделяется элементарное количество теплоты ∆Q=i²R∆t то есть количество теплоты пропорциональное произведению i²R.

7. Закон Джоуля-Ленца для цепи постоянного и переменного токов.

Закон Джоуля-Ленца.Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.

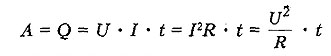
По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время.

РАБОТА ПОСТОЯННОГО ТОКА

Работа тока - работа электрического поля по переносу электрических зарядов вдоль проводника;

Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого работа совершалась.

По закону сохранения энергии:

работа равна изменению энергии участка цепи, поэтому выделяемая проводником энергия

равна работе тока.

РАБОТА Переменного ТОКА

dQ/(dtdV)=pj²

Эта формула справедлива как для постоянного, так и для переменногот ока изменяющегося по любому закону.

8. Активная, реактивная, комплексная и полная мощность потребителя электрической энергии.

Мощность (электрическая мощность) – физическая и техническая величина в цепях электрического тока.

Полная мощность (“S”), кажущаяся мощность, величина, равная произведению действующих значений периодического электрического тока в цепи “I” и напряжения “U” на её зажимах: S=U*I; для синусоидального тока (в комплексной форме) равна (P2 + Q2), где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0). Измеряется в ВА (Вольт*Ампер), кВА (Кило*Вольт*Ампер).

Мощность полная – вычисляемое значение (или результат измерений), необходимое для определения, например, параметров электрических генераторов. Значение полной мощности в цепи переменного тока есть произведение эффективных значений тока и напряжения.

Активная мощность (“P”), среднее за период значение мгновенной мощности переменного тока; характеризует среднюю скорость преобразования электромагнитной энергии в другие формы (тепловую, механическую, световую и т. д.). Измеряется в Вт (W, – ваттах).

Для синусоидального тока активная мощность равна произведению действующих (эффективных) значений тока “I” и напряжения “U” на косинус угла сдвига фаз между ними: P = I*U*Cos ф.

В любой электрической цепи как синусоидального, так и несинусоидального тока, активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи. С полной мощностью («S») активная мощность связана соотношением: P = S*Сos ф.

Реактивная мощность («Q»), величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока. Реактивная мощность «Q» для синусоидального тока равна произведению действующих значений напряжения “U” и тока “I”, умноженному на синус угла сдвига фаз между ними: Q = U*I*Sin ф.

Реактивная мощность, потребляемая в электрических сетях, вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). Реактивная мощность потребляется индуктивной нагрузкой (электродвигателями переменного тока, трансформаторами).

Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:

Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует (активно-индуктивная нагрузка), для которого имеем: