- •Часть 1
- •Линейные электрические цепи постоянного
- •И однофазного синусоидального токов
- •Оглавление
- •1. Линейные электрические цепи постоянного тока
- •1.1. Электрическая цепь и ее элементы
- •1.2. Закон Ома для участка цепи с эдс
- •1.3. Расчет сложных электрических цепей постоянного тока
- •1.3.2. Метод узловых потенциалов
- •1.3.3. Метод контурных токов
- •1.3.4. Метод наложения
- •1.4. Пассивный и активный двухполюсники. Теорема об активном двухполюснике
- •1.5. Метод эквивалентного генератора
- •1.6. Линия электропередачи постоянного тока
- •2. Электрические цепи однофазного синусоидального тока
- •2.1. Закон электромагнитной индукции
- •2.2. Получение синусоидальной эдс. Характеристики синусоидальных величин. Обозначения в цепях переменного тока
- •2.3. Действующее значение переменного тока
- •2.4. Представление синусоидальной функции времени вращающимся вектором. Векторные диаграммы
- •2.5. Основные сведения о комплексных числах
- •2.6. Представление синусоидальных функций времени комплексными числами
- •2.7. Способы задания синусоидального тока
- •2.8. Законы Кирхгофа в цепях синусоидального тока. Методы расчета цепей синусоидального тока
- •2.9. Понятие об активном сопротивлении. Синусоидальный ток в активном сопротивлении
- •2.10. Самоиндукция. Индуктивность. Синусоидальный ток в индуктивности
- •2.11. Синусоидальный ток в емкости
- •2.12. Последовательное соединение активного сопротивления, индуктивности и емкости
- •2.13. Параллельное соединение активного сопротивления, индуктивности и емкости
- •2.14. Пассивный двухполюсник в цепи синусоидального тока. Эквивалентные сопротивления и проводимости
- •2.15. Закон Ома в символической форме для произвольной цепи
- •2.16. О расчете цепей синусоидального тока
- •2.17. Резонансы в электрических цепях
- •2.18. Энергия и мощность в цепи синусоидального тока
2.3. Действующее значение переменного тока
Понятие действующего значения тока вводится в связи с необходимостью производства измерений. Что измерять у переменного тока? Если бы мы имели дело только с синусоидами – кривыми одной формы, то можно было бы измерять амплитуды. Но на практике встречаются самые разные кривые, и может оказаться так, что два различных по форме тока имеют одинаковые амплитуды, хотя очевидно, что на электрическую цепь они будут оказывать разное воздействие.
Поэтому наиболее целесообразно оценивать величину тока по той работе, которую он совершает. При такой оценке действие переменного тока сравнивается с аналогичным действием постоянного тока. Например, если некоторый переменный ток выделяет на участке цепи такое же количество тепла, что и постоянный ток силой 10 ампер, то говорят, что величина этого переменного тока составляет 10 ампер. Это значение тока и называют действующим.
Итак, действующим значением переменного тока называется численное значение такого постоянного тока, который за время, равное одному периоду, выделяет в сопротивлении такое же количество тепла, что и ток переменный.
Таким образом, для оценки величины переменного тока мы должны сделать следующее.
1.
Определить количество теплоты,
выделяющейся в сопротивлении R
за время Т
при протекании переменного тока i.
Это количество теплоты равно
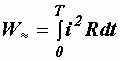 .
.
`
2. Подобрать такой постоянный ток I,
который за то же время Т
в том же сопротивлении R
выделяет такое же количество тепла. При
постоянном токе оно равно
![]() .
.
3. Приравнять W и W=:
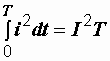 ,
,
откуда
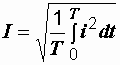 .
(2.5)
.
(2.5)
Последняя формула и определяет действующее значение переменного тока.
Пример 2.1. На вход некоторой цепи подается импульсное напряжение треугольной формы (рис. 2.4, а). Чему равно его действующее значение?
Р е ш е н и е.
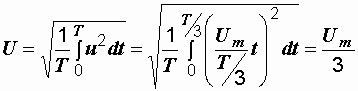 .
.

Рис. 2.4. Переменные напряжения различной формы
Пример 2.2. На рис. 2.4, б показана кривая напряжения на выходе схемы однофазного однополупериодного выпрямления. Чему равно действующее значение напряжения, если его амплитудное значение Um составляет 311 В?
Р е ш е н и е.
 155,5
В.
155,5
В.
Пример 2.3. Определить действующее значение синусоидального тока
![]() .
.
Р е ш е н и е.
 .
.
Рассмотренные примеры показывают, что действующее значение переменного тока зависит от его формы.
У
синусоидального тока оно равно амплитуде,
деленной на
![]() .
.
2.4. Представление синусоидальной функции времени вращающимся вектором. Векторные диаграммы
Пусть в прямоугольной системе координат имеется вектор длиной Im, расположенный под углом к горизонтальной оси (рис. 2.5). Заставим этот вектор вращаться против часовой стрелки c угловой скоростью . Тогда за время t он повернется на угол t.
Рис. 2.5. Вращающийся вектор |
Проекцию вектора на вертикальную ось
обозначим i.
Из треугольника oab
она равна
|
Обычно вектор при этом показывается не в произвольный момент времени t, а в начальный (t = 0), когда его угол наклона к горизонтальной оси равен начальной фазе.
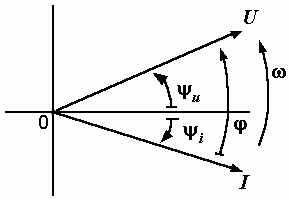
Теперь по уравнениям (2.3) построим векторную диаграмму двух векторов – тока и напряжения (рис. 2.6).
Рис. 2.6. Векторная диаграмма тока и напряжения |
Длины векторов равны действующим значениям, углы их наклона к горизонтальной оси – начальным фазам, а угол между векторами, равный разности начальных фаз u и i, в соответствии с уравнением (2.4) определяет сдвиг фаз напряжения и тока. Подчеркиваем, что на диаграмме стрелка, отмечающая угол , всегда направляется от вектора тока к вектору напряжения. Сейчас она направлена в положительном направлении – против часовой стрелки. |
Векторная диаграмма дает наглядное представление об отставании одних величин и опережении других. Если вращать картинку, показанную на рис. 2.6, против часовой стрелки, то вектор тока будет отставать от напряжения на угол . Так как при вращении длины векторов и угол между ними не меняются, то в том случае, когда начальные фазы напряжения и тока нас не интересуют, мы можем изображать диаграмму без осей и располагать ее так, как нам удобно (рис. 2.7).
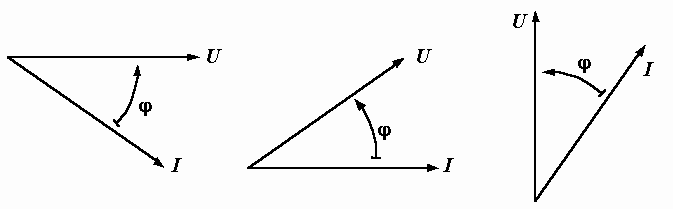
Рис. 2.7. Варианты построения векторной диаграммы