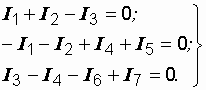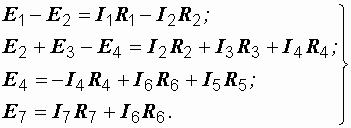1.2. Закон Ома для участка цепи с эдс

    На практике часто встречается задача, когда требуется определить ток в некоторой ветви при известных ее параметрах и потенциалах ее зажимов.

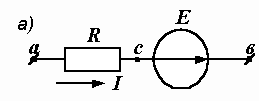
    Пусть в схеме на рис. 1.8, а заданы R, E,  _a,  _b, и требуется определить ток.

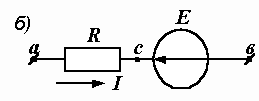
Рис. 1.8. Варианты ветви с ЭДС

    Между R и E отметим промежуточную точку с и выразим ее потенциал через потенциалы точек а и b.

    Так как в резисторе ток протекает слева направо, то потенциал точки а выше потенциала точки с на величину падения напряжения в активном сопротивлении:

 _a =  _с + IR.                                                          (1.4)

    Точка b находится на положительном полюсе источника, а с – на отрицательном. Поэтому

 _b =  _с + E.                                                         (1.5)

    Беря разность левых и правых частей выражений (1.4) и (1.5), получим

 _a –  _b = IR – Е,

откуда

.

    Для цепи на рис. 1.8, б после аналогичных рассуждений будем иметь

I = ( _a –  _b – E) G.

    В двух последних формулах ЭДС записывается с плюсом, если ее направление на схеме совпадает с направлением тока, и с минусом – в противоположном случае.

 

1.3. Расчет сложных электрических цепей постоянного тока

1.3.1. Метод непосредственного применения законов Кирхгофа

    Этот метод сводится к решению системы уравнений, количество которых равно числу неизвестных токов (числу ветвей). Покажем его применение на примере схемы, изображенной на рис. 1.9.

Рис. 1.9. Сложная электрическая цепь

    Первый закон Кирхгофа: в узле электрической цепи алгебраическая сумма токов равна нулю.

    Произвольно задавшись направлениями токов в ветвях и принимая токи, подтекающие к узлу, положительными, а оттекающие от узла – отрицательными, записываем:

узел а: узел в: узел с:

(1.6)

    Число независимых уравнений в первом законе Кирхгофа – на единицу меньше числа узлов, поэтому для последнего узла d уравнение не пишем.

    В заданной схеме семь ветвей, семь неизвестных токов. Система (1.6) содержит только три уравнения. Недостающие четыре записываем по второму закону Кирхгофа.

    Второй закон Кирхгофа: в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура.

    Число уравнений, составляемых по этому закону, равно числу взаимно независимых контуров. При рассмотрении схемы каждый последующий контур является независимым относительно предыдущих, если он отличается от них хотя бы одной новой ветвью. В заданной схеме таких контуров четыре. Они отмечены пронумерованными дугообразными стрелками. Любой другой контур новых ветвей не содержит, поэтому не является независимым. Дугообразные стрелки показывают произвольно выбранные направления обхода контуров. Если направления ЭДС и токов совпадают с направлением обхода контура, то они записываются с плюсом, если не совпадают – то с минусом.

контур 1: контур 2: контур 3: контур 4:

(1.7)

    Системы (1.6) и (1.7) дают достаточное количество уравнений для отыскания всех неизвестных токов.