
- •Часть 1
- •Линейные электрические цепи постоянного
- •И однофазного синусоидального токов
- •Оглавление
- •1. Линейные электрические цепи постоянного тока
- •1.1. Электрическая цепь и ее элементы
- •1.2. Закон Ома для участка цепи с эдс
- •1.3. Расчет сложных электрических цепей постоянного тока
- •1.3.2. Метод узловых потенциалов
- •1.3.3. Метод контурных токов
- •1.3.4. Метод наложения
- •1.4. Пассивный и активный двухполюсники. Теорема об активном двухполюснике
- •1.5. Метод эквивалентного генератора
- •1.6. Линия электропередачи постоянного тока
- •2. Электрические цепи однофазного синусоидального тока
- •2.1. Закон электромагнитной индукции
- •2.2. Получение синусоидальной эдс. Характеристики синусоидальных величин. Обозначения в цепях переменного тока
- •2.3. Действующее значение переменного тока
- •2.4. Представление синусоидальной функции времени вращающимся вектором. Векторные диаграммы
- •2.5. Основные сведения о комплексных числах
- •2.6. Представление синусоидальных функций времени комплексными числами
- •2.7. Способы задания синусоидального тока
- •2.8. Законы Кирхгофа в цепях синусоидального тока. Методы расчета цепей синусоидального тока
- •2.9. Понятие об активном сопротивлении. Синусоидальный ток в активном сопротивлении
- •2.10. Самоиндукция. Индуктивность. Синусоидальный ток в индуктивности
- •2.11. Синусоидальный ток в емкости
- •2.12. Последовательное соединение активного сопротивления, индуктивности и емкости
- •2.13. Параллельное соединение активного сопротивления, индуктивности и емкости
- •2.14. Пассивный двухполюсник в цепи синусоидального тока. Эквивалентные сопротивления и проводимости
- •2.15. Закон Ома в символической форме для произвольной цепи
- •2.16. О расчете цепей синусоидального тока
- •2.17. Резонансы в электрических цепях
- •2.18. Энергия и мощность в цепи синусоидального тока
2.14. Пассивный двухполюсник в цепи синусоидального тока. Эквивалентные сопротивления и проводимости
На
рис. 2.36 показан пассивный двухполюсник,
состоящий из активных и реактивных
элементов. Действующие значения
напряжения
![]() ,
тока
,
тока
![]() и
угол сдвига фаз между ними
и
угол сдвига фаз между ними
![]() известны.
известны.
Построим по этим значениям векторную
диаграмму и, спроектировав вектор
напряжения на вектор тока и
перпендикулярное к нему направление,
получим треугольник напряжений,
образованный сторонами
Как
и раньше,
и
будем
называть активной и реактивной
составляющими напряжения. Изображенная
в таком виде диаграмма соответствует
схеме, показанной на рис. 2.37, б.
Действительно, для нее
|
Рис. 2.36. Пассивный двухполюсник |
Схема
называется последовательной схемой
замещения или последовательной
эквивалентной схемой пассивного
двухполюсника, а ее параметры
![]() ,
,
![]() и
и
![]() –
эквивалентными сопротивлениями
двухполюсника.
–
эквивалентными сопротивлениями
двухполюсника.
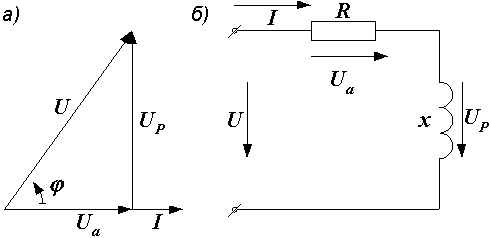
Рис. 2.37. Векторная диаграмма и соответствующая ей последовательная эквивалентная схема
Треугольник, образованный сторонами , и и подобный треугольнику напряжений, представляет собой треугольник сопротивлений (рис. 2.28, б), для которого справедливы формулы (2.27).
Теперь
разложим в е к т о р т о к а на две
составляющие – активную
![]() ,
направленную по вектору напряжения, и
реактивную
,
направленную по вектору напряжения, и
реактивную
![]() ,
перпендикулярную к нему (рис. 2.38, а).
Такой векторной диаграмме соответствует
параллельная схема замещения двухполюсника
(рис. 2.38, б).
Ее параметры
,
перпендикулярную к нему (рис. 2.38, а).
Такой векторной диаграмме соответствует
параллельная схема замещения двухполюсника
(рис. 2.38, б).
Ее параметры
![]() ,
,
![]() и
и
![]() называются
эквивалентными проводимостями. Токи в
элементах
и
мы
и представляем как активную и реактивную
составляющие общего тока:
называются
эквивалентными проводимостями. Токи в
элементах
и
мы
и представляем как активную и реактивную
составляющие общего тока:
![]() ,
,
![]() .
Из треугольника токов (рис. 2.38, а)
получается треугольник проводимостей
(рис. 2.32, б),
стороны которого связаны между собой
формулами (2.29).
.
Из треугольника токов (рис. 2.38, а)
получается треугольник проводимостей
(рис. 2.32, б),
стороны которого связаны между собой
формулами (2.29).
а) б)

Рис. 2.38. Параллельная эквивалентная схема и ее векторная диаграмма
Получим условия эквивалентности приведенных схем.
Для
последовательной цепи
,
для параллельной
![]() ,
а так как токи и напряжения в обеих
схемах одинаковы, то
,
а так как токи и напряжения в обеих
схемах одинаковы, то
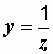 и
и
 ,
(2.30)
,
(2.30)
т.е. в любой электрической цепи полная проводимость есть величина, обратная полному сопротивлению.
Из сопоставления формул (2.27) и (2.29) можно записать:
 и
и
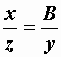 .
.
Рассматривая последние выражения совместно с (2.30), можно получить две группы формул:
Формулы перехода от последовательной эквивалентной схемы к параллельной: |
Формулы перехода от параллельной эквивалентной схемы к последовательной: |
|
|
Обращаем внимание на то, что каждая из проводимостей G и B зависит от обоих сопротивлений – активного и реактивного. В свою очередь, каждое из сопротивлений определяется обеими проводимостями. Соотношения G = 1/R и B = 1/x справедливы только в частном случае, первое – при х = 0, второе – при R = 0.
Следует отметить, что активная и реактивная составляющие напряжения и тока физически не существуют, измерить их нельзя. Они относятся только к соответствующим эквивалентным схемам замещения и находятся расчетом. Более того, проектируя, например, вектор тока на различные напряжения, мы получим для него разные составляющие.
Пример 2.15. Найти общее сопротивление цепи, состоящей из параллельно соединенных активного R = 30 Ом и индуктивного х = 40 Ом сопротивлений (рис. 2.39, а).

Рис. 2.39. Схемы к примерам 2.15–2.17
Р е ш е н и е. Так как в левой ветви реактивного сопротивления нет, то ее проводимость в соответствии с (2.31) равна G = 1/R. Аналогично, во второй ветви B = 1/x. Полная проводимость цепи . В соответствии с (2.30) полное сопротивление цепи
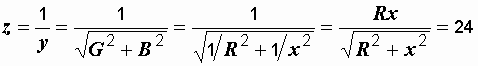 Ом.
Ом.
Пример 2.16. Рассчитать общее сопротивление цепи, состоящей из параллельно соединенных индуктивности L = 0,478 Гн и емкости С = 31,85 мкФ (рис. 2.39, б). Частота питающего напряжения f = 50 Гц.
Р е ш е н и е. Определяем сопротивления ветвей:
![]() Ом,
Ом,
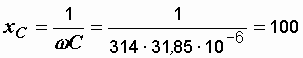 Ом.
Ом.
Так как в ветвях отсутствуют активные сопротивления, то их проводимости соответственно равны BL = 1/xL и BC = 1/xС. Полная эквивалентная проводимость цепи не содержит активной составляющей и равна
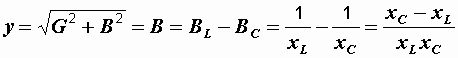 .
.
Полное эквивалентное сопротивление
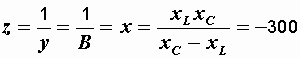 Ом.
Ом.
В рассматриваемой цепи активных элементов нет, она носит чисто реактивный характер. Он может быть индуктивным или емкостным. Знак минус в ответе свидетельствует о последнем, т.е. вся цепь может быть заменена конденсатором емкостью
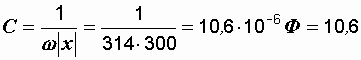 мкФ.
мкФ.
Пример 2.17. Амперметр А, вольтметр V и фазометр , включенные в цепь катушки (рис. 2.39, в), дали следующие показания: U = 220 В, I = 4,4 А, cos = 0,8. Частота питающего напряжения 50 Гц. Определить параметры последовательной и параллельной схем замещения катушки.
Р е ш е н и е. Находим параметры последовательной эквивалентной схемы:
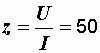 Ом,
Ом,
![]() Ом,
Ом,
![]() Ом.
Ом.
Рассчитываем элементы параллельной эквивалентной схемы:
 См,
См,
![]() См,
См,
![]() См.
См.
После определения эквивалентных сопротивлений эквивалентные проводимости можно было найти иначе, по формулам (2.31):
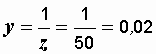 См,
См,
 См,
См,
 См.
См.
Пример 2.18. Рассчитать токи в схеме, приведенной на рис. 2.40.
|
Рис. 2.40. Расчетная схема |
Р е ш е н и е. Определяем полные сопротивления второй и третьей ветвей:
![]() Ом,
Ом,
![]() Ом.
Ом.
Преобразуем эти ветви в эквивалентные параллельные (рис. 2.41, а).
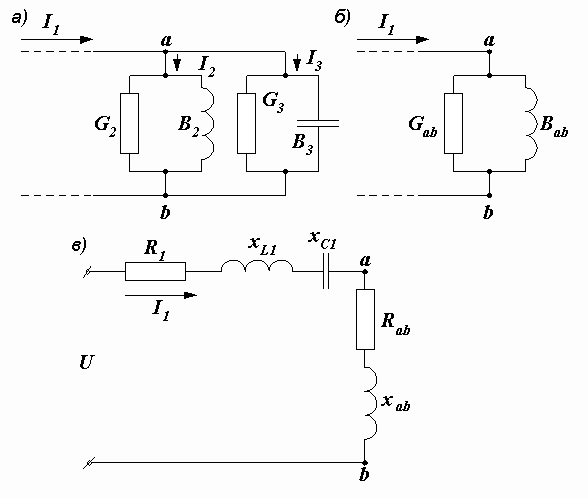
Рис. 2.41. Преобразования электрической цепи
Их проводимости:
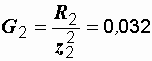 См,
См,
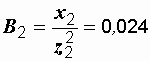 См,
См,
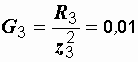 См,
См,
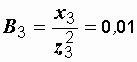 См.
См.
Суммируем активные и реактивные проводимости параллельных ветвей:
![]() См,
См,
![]() См
(см. рис. 2.41, б).
См
(см. рис. 2.41, б).
Определяем
эквивалентные сопротивления участка
![]() (рис.
2.41, в):
(рис.
2.41, в):
 Ом,
Ом,
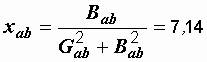 Ом,
Ом,
![]() Ом,
Ом,
и полное сопротивление цепи:
![]() Ом.
Ом.
Ток на входе цепи I1 = U/z = 220/41,53 = 5,297 A.
Напряжение
на участке
![]() Uab=
I1zab=
119,7 В.
Uab=
I1zab=
119,7 В.
Токи второй и третьей ветвей:
 А,
А,
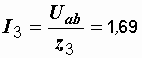 А.
А.
Еще
раз напоминаем, что для численных
значений токов и напряжений законы
Кирхгофа неприменимы:
![]() .
.

 (2.31)
(2.31)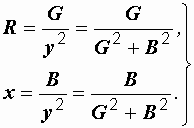 (2.32)
(2.32)