
- •Часть 1
- •Линейные электрические цепи постоянного
- •И однофазного синусоидального токов
- •Оглавление
- •1. Линейные электрические цепи постоянного тока
- •1.1. Электрическая цепь и ее элементы
- •1.2. Закон Ома для участка цепи с эдс
- •1.3. Расчет сложных электрических цепей постоянного тока
- •1.3.2. Метод узловых потенциалов
- •1.3.3. Метод контурных токов
- •1.3.4. Метод наложения
- •1.4. Пассивный и активный двухполюсники. Теорема об активном двухполюснике
- •1.5. Метод эквивалентного генератора
- •1.6. Линия электропередачи постоянного тока
- •2. Электрические цепи однофазного синусоидального тока
- •2.1. Закон электромагнитной индукции
- •2.2. Получение синусоидальной эдс. Характеристики синусоидальных величин. Обозначения в цепях переменного тока
- •2.3. Действующее значение переменного тока
- •2.4. Представление синусоидальной функции времени вращающимся вектором. Векторные диаграммы
- •2.5. Основные сведения о комплексных числах
- •2.6. Представление синусоидальных функций времени комплексными числами
- •2.7. Способы задания синусоидального тока
- •2.8. Законы Кирхгофа в цепях синусоидального тока. Методы расчета цепей синусоидального тока
- •2.9. Понятие об активном сопротивлении. Синусоидальный ток в активном сопротивлении
- •2.10. Самоиндукция. Индуктивность. Синусоидальный ток в индуктивности
- •2.11. Синусоидальный ток в емкости
- •2.12. Последовательное соединение активного сопротивления, индуктивности и емкости
- •2.13. Параллельное соединение активного сопротивления, индуктивности и емкости
- •2.14. Пассивный двухполюсник в цепи синусоидального тока. Эквивалентные сопротивления и проводимости
- •2.15. Закон Ома в символической форме для произвольной цепи
- •2.16. О расчете цепей синусоидального тока
- •2.17. Резонансы в электрических цепях
- •2.18. Энергия и мощность в цепи синусоидального тока
2.13. Параллельное соединение активного сопротивления, индуктивности и емкости
Рассмотрим схему, состоящую из параллельно соединенных активного и реактивных элементов (рис. 2.31, а).
Требуется по известным G, ВL, ВC, U рассчитать токи. Как и прежде, задачу будем решать двумя методами.
1. М е т о д в е к т о р н ы х д и а г р а м м.
Токи
ветвей находятся сразу:
![]() ,
,
![]() ,
,
![]() .
.
Для определения общего тока необходимо построить векторную диаграмму (рис. 2.31, б). Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей. Из векторной диаграммы имеем
![]()
или
![]() ,
,
где
![]() –
полная проводимость цепи, равная
–
полная проводимость цепи, равная
![]() .
.
Разность
индуктивной и емкостной проводимостей
представляет собой общую реактивную
проводимость цепи
![]() .
.

Рис. 2.31. Электрическая цепь и ее векторная диаграмма
Векторы
токов на диаграмме образуют треугольник
токов. Его горизонтальный катет,
представляющий проекцию вектора тока
на вектор напряжения, называется активной
составляющей тока и равен току в активном
элементе цепи:
![]() (рис.
2.32, а).
Проекция вектора тока на направление,
перпендикулярное напряжению, – это
реактивная составляющая тока. Она равна
суммарному току реактивных элементов
(рис.
2.32, а).
Проекция вектора тока на направление,
перпендикулярное напряжению, – это
реактивная составляющая тока. Она равна
суммарному току реактивных элементов
![]() и
определяется как разность длин векторов:
и
определяется как разность длин векторов:
![]()
![]() (см.
рис. 2.31, б
и 2.32, а).
(см.
рис. 2.31, б
и 2.32, а).

Рис. 2.32. Треугольники токов и проводимостей
Разделив
все стороны треугольника токов на
![]() ,
получим треугольник проводимостей
(рис. 2.32, б),
стороны которого связаны следующими
соотношениями:
,
получим треугольник проводимостей
(рис. 2.32, б),
стороны которого связаны следующими
соотношениями:
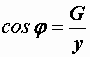 ,
,
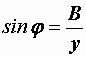 ,
,
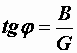 ,
,
![]() .
(2.29)
.
(2.29)
2. С и м в о л и ч е с к и й м е т о д.
Раньше были получены следующие формулы:
![]() ,
,
![]() ,
,
![]() .
.
Подставляя их в уравнение первого закона Кирхгофа, получаем:
![]() или
или
![]() ,
,
где
![]() –
комплексная проводимость цепи, равная
–
комплексная проводимость цепи, равная
![]()
Пример
2.12.
Для цепи, показанной на рис. 2.33, а,
рассчитать токи, угол сдвига фаз между
током и напряжением на входе цепи,
построить векторную диаграмму. Числовые
значения параметров цепи:
![]() В,
В,
![]() Ом,
Ом,
![]() мкФ,
мкФ,
![]() с-1.
с-1.
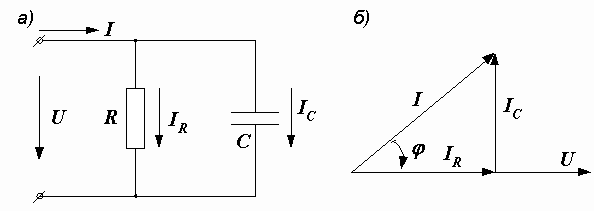
Рис. 2.33. Электрическая цепь и ее векторная диаграмма
Р е ш е н и е.
 А,
А,
 Ом,
Ом,
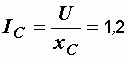 А,
А,
![]() А.
А.
Векторная диаграмма приведена на рис. 2.33, б.
Угол
сдвига фаз
 .
.
Величину общего тока можно найти иначе:
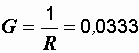 См,
См,
 См,
См,
![]() См,
См,
![]() А.
А.
Пример 2.13. Начертить цепь, векторная диаграмма которой изображена на рис. 2.34, а.
Р е ш е н и е задачи показано на рис. 2.34, б.

Рис. 2.34. Векторная диаграмма и соответствующая ей электрическая цепь
Пример 2.14. Чему равно показание амперметра А на входе цепи в схемах рис. 2.35, если амперметры А1 и А2 во всех случаях показывают соответственно 4 и 3 А?

Рис. 2.35. Измерение тока в электрической цепи
Предлагаем для каждого случая самостоятельно построить векторную диаграмму и убедиться в правильности приведенных ответов: а) 5А, б) 7А, в) 1А.
