Тема 3.5. Анализ хозяйственной деятельности предприятия

3.5.1. Виды и методы анализа

3.5.2. Система показателей эффективности хозяйственной деятельности фирм

3.5.1. Виды и методы анализа

Анализ является одной из основных функций управления и со­стоит из разъединения целостной совокупности на отдельные ча­сти, изучая которые получают представление о развитии всей со­вокупности под влиянием как внутренних, так и внешних факто­ров.

В процессе анализа выявляют­ся резервы, причинно-следственные связи и факторы, которые можно использовать для роста эффективности деятельности фир­мы. Аналитики разрабатывают методики по реализации выявлен­ных резервов и факторов, практическому использованию резуль­татов анализа в текущей и перспективной управленческой дея­тельности фирмы.

Методы анализа хозяйственной деятельности — это совокупность приемов, применяемых для обработки информации о работе предприя­тия.

Традиционными общими способами (приемами) обработки, изучения и обобщения информации при анализе являются сравне­ние, сводка и группировка, балансовый метод, графический ана­лиз, табличный метод, методы определения относительных и сред­них величин, моделирование и оптимизация.

Сравнение — это прием, позволяющий выразить характеристику одного явления через другое. В практике анализа хозяйственной де­ятельности предприятия производится сравнение анализируемых показателей с нормативными, отчетными, плановыми, максималь­ными, минимальными, оптимальными, с показателями предше­ствующих периодов (ретроспективный анализ) и т. д. Применение приема сравнения требует приведения показателей в сопоставимый вид. Сопоставимость показателей предполагает тождество объем­ных и стоимостных характеристик, структурных составляющих, ра­венство промежутков времени, за которые вычислены сравнивае­мые показатели.

Группировка — это прием, с помощью которого генеральная совокупность показателей разбивается на относительно однородные группы с целью обобщения и типизации признаков, характеризую­щих группы и всю совокупность анализируемого объекта. Например, группировка основных средств предприятий по возрастному составу (до 10 лет, 10—20 и свыше 20 лет) дает представление об их структуре и возможностях наращивания производственного потенциала. В то же время группировка основных средств по их типам (здания, со­оружения, оборудование, транспорт и т. д.) характеризует соотно­шение их активной и пассивной части, прогрессивность производ­ственного потенциала.

Группировки осуществляются, как правило, в табличной форме. Таблицы, в которых отражаются соотношения, пропорции двух групп взаимосвязанных показателей, итоги которых равны, называют ба­лансовыми. Балансовые таблицы широко используются предприяти­ями и в целом по отраслям, регионам, и в национальном счетовод­стве. Это балансы имущества и обязательств, балансы доходов и рас­ходов, балансы поступлений и использования товарно-материальных ценностей и т. д.

Данные таблиц могут быть использованы для представления показателей в графическом виде (графический анализ). Основными формами графического анализа являются графики и диаграммы. Они бывают линейными, плоскостными и объемными.

По способу построения графики могут подразделяться на диаг­раммы и статистические карты. Диаграммы сравнения показывают соотношения разных объектов по каким-либо пока­зателям (полосовые и столбиковые диаграммы). Диаграммы дина­мики позволяют анализировать явления за установленные периоды (столбиковые, круговые, квадратные, фигурные и другие гра­фики), где на оси абсцисс, как правило, откладываются периоды времени, а на оси ординат — уровень показателей.

В анализе хозяйственной деятельности часто используются гра­фики контроля. При необходимости выделения проблемных вопро­сов, в том числе при контроле качества продукции, используют диаграммы Парето. С их помощью выделяется степень важности каж­дого из факторов.

Все вышеперечисленные методы, используемые в анализе хозяйственной деятельности предприятия, должны использовать показатели, имеющие количественную определенность, которая вы­ражается в абсолютных и относительных величинах. Абсолютные величины показателей характеризуют явления в единицах меры, веса, объема, площади, стоимости и т. д. Относительные величины показателей характеризуют соотношение изучаемого явления с ба­зовым, сравниваемым. Отношение выражается в форме коэффици­ентов, удельных весов, процентов.

В анализе используются разные виды относительных величин (изменение планового показателя в динамике по отношению к базовому, цепным методом, изменение структуры, изменение эффективности). Особое место среди относительных показателей в анализе занимают средние величины. Они используются для ха­рактеристики совокупности однородных явлений по какому-либо признаку. В каждом конкретном случае могут рассчитываться раз­ные типы средних величин: средняя арифметическая, средняя арифметическая взвешенная, средняя гармоническая, средняя геометрическая, средние хронологические и др. Условия применения метода средних величин — наличие вариации уровня какого-либо признака у совокупности однородных явлений.

Простая средняя арифметическая применяется, когда есть дан­ные только об отдельных значениях варьирующего признака и о числе единиц совокупности. Простая средняя арифметическая ве­личина признака выражается следующей формулой:

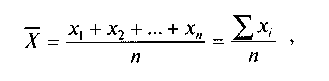
,где — средний размер признака;

х1, х2, ..., хn — индивидуальные значения признака;

n — число индивидуальных значений призна­ка;

хi — индивидуальные значения i-го признака.

Средняя арифметическая взвешенная определяется, когда варьи­рующий признак имеет вес (числовое значение) в общей совокуп­ности. Формула средней арифметической взвешенной представля­ется в виде:

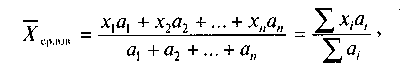
, где аi— вес признака.

Пример. На обследованных предприятиях отрасли численность работ­ников составляет соответственно до 12 человек, до 30, до 98, до 150 и до 500 человек. Причем предприятий с численностью работающих до 12 чело­век насчитывается 3, до 30 человек — 2, до 98 человек — 5, до 150 человек— 2 и до 500 человек — 1. Определить среднюю арифметичес­кую взвешенную величину численности персонала первого типа предпри­ятий в отрасли.

Средняя арифметическая взвешенная величина численности персона­ла первого предприятия в отрасли будет равна:

Средняя гармоническая определяется, когда значение варьирую­щего признака обратно пропорционально величине признака или когда в качестве веса выступает произведение значений варьирую­щего признака на количество единиц, обладающих признаками. Средняя гармоническая рассчитывается по формуле:

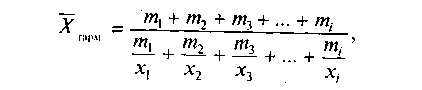
,где mi - веса средней гармонической;

хi - отдельные варианты признака.

Обобщенная формула средней гармонической имеет вид:

Пример. Имеется три сорта конфет. Цена первого сорта (за 1 кг) -80 руб., второго - 50 руб., третьего - 40 руб. По накладным числится конфет первого сорта на 400 руб., второго - на 150 руб., третьего - на 40 руб. Определить среднюю цену 1 кг смеси конфет.

Средняя цена 1 кг смеси конфет определяется по формуле средней гармонической:

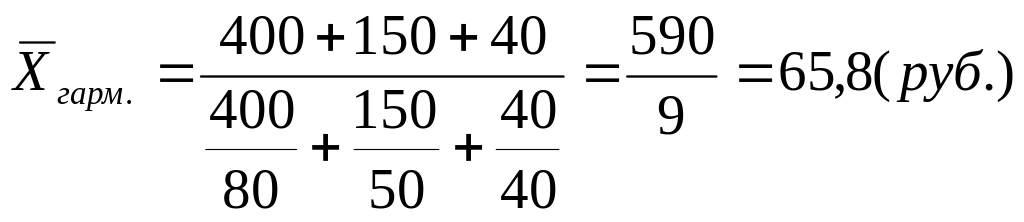
Средняя геометрическая применяется при исчислении средних темпов роста и рассчитывается по формуле:

,где n — число вариантов;

хn — значение варианта признака.

Пример. Имеется динамический ряд темпов роста за 1990—2000 гг. (табл.1). Определить средний темп роста за два года.

Таблица 1

Показатель	1990	1 992	1994	1996	1998	2000
Темп роста, %	100	120	134	120	98	90

Средний темп роста за два года определяется по формуле средней гео­метрической:

Средняя хронологическая интервального ряда, если все интервалы равны, исчисляется по формуле простой средней арифметической:

Пример. В 1996, 1997, 1998, 1999 и 2000 гг. на предприятии произведено соответственно 200, 250, 260, 270, 275 штук изделий. Определить средне­годовой уровень производства за 1996—2000 гг.

Среднегодовой уровень производства за 1996—2000 гг. определяется как средняя хронологическая интервального ряда:

Средняя хронологическая моментного ряда определяется по формуле:

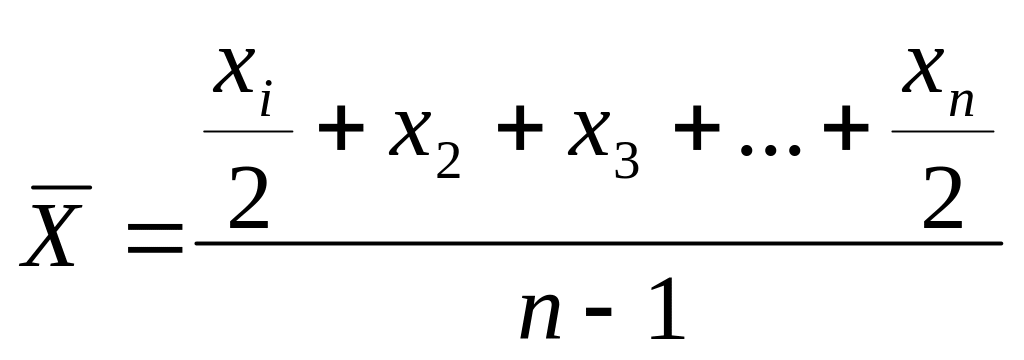
,где хn — уровень ряда;

n — число уровней ряда.

Пример. Стоимость основных фондов на начало года составила 1,2 млн руб., на конец января — 1,3 млн, февраля — 1,4 млн, марта — 1,5 млн, апреля — 1,4 млн, мая — 1,3 млн, июня — 1,2 млн, июля — 1,4 млн, августа — 1,5 млн, сентября — 1,6 млн, октября — 1,4 млн, ноября — 1,5 млн, на конец декабря — 1,7 млн руб. Определить среднего­довую стоимость основных фондов.

Среднегодовая стоимость основных фондов составит:

С помощью вышеперечисленных приемов осуществляются ана­лиз, диагностика и оценка состояния хозяйственной деятельности фирмы. Однако на практике достаточно часто необходимо макси­мизировать, минимизировать или рационализировать те или иные факторы развития. Тогда применяются экономико-математические методы, к которым относятся методы линейного программирования, динамического программирования, математическая теория игр, матричные методы анализа, теория нечетных множеств, математи­ческая теория массового обслуживания и др.

Методы линейного программирования основаны на решении сис­темы линейных уравнений (с преобразованием в уравнения и нера­венства), когда зависимость между изучаемыми явлениями функ­циональна. К ним относятся симплексный и распределительный методы. С помощью названных методов решаются задачи рацио­нального раскроя материалов (с оптимальным выходом заготовок), определения минимальной стоимости при заданном количестве, оптимальная производительность при заданном ассортименте, транс­портная задача, задачи рационального прикрепления потребите­лей к изготовителям (продавцам) и т. д.

Методы динамического программирования применяются при решении оптимизационных задач, в которых целевая функция или ограничения, или и то и другое характеризуются нелинейными за­висимостями.

Математическая теория игр исследует оптимальные стратегии в ситуациях игрового характера. К ним относятся ситуации, связан­ные с выбором наивыгоднейших производственных решений, сис­темы научных и хозяйственных экспериментов, с организацией статистического контроля, хозяйственных взаимоотношений и т. д.

Матричные методы анализа основаны на линейной и векторно-матричной алгебре. Применяются для изучения сложных и высоко­размерных структур как на отраслевом уровне, так и на уровне предприятий и их объединений. Примером применения матричных методов может служить модель Леонтьева многоотраслевой эконо­мики, современные методы решения задач межотраслевого балан­са и др.

Теория нечетких множеств относится к числу прикладных математических моделей, поскольку направлена на решение приклад­ных задач и возникла из чисто практических потребностей, а использует математические методы.

Математическая теория массового обслуживания облегчает ре­шение задач обслуживания, например, обслуживания кораблей в порту, рабочих в инструментальной кладовой, клиентов в сервис­ных центрах.