10. Дифференциальные модели. Методы. Задачи. Модель математического маятника.
Динамика простого гармонического движения
Для колебания в одномерном пространстве, учитывая Второй закон Ньютона (F = m d²x/dt²) и закон Гука (F = −kx, как описано выше), имеем линейное дифференциальное уравнение второго порядка:
Где
m — это масса тела, x — его перемещение
относительно положения равновесия, k —
постоянная (коэффициент жёсткости
пружины).
Решение этого дифференциального уравнения является синусоидальным; одно из решений таково: x(t) = Acos(ωt + φ), где A, ω, и φ — это постоянные величины, и положение равновесия принимается за начальное. Каждая из этих постоянных представляет собой важное физическое свойство движения:
A — это амплитуда, ω = 2πf — это круговая частота, и φ — начальная фаза.
Используя
приёмы дифференциального исчисления,
скорость и ускорение как функция времени
могут быть найдены по формулам:
Ускорение
может быть также выражено как функция
перемещения:
Поскольку
ma = −mω²x = −kx, то
Учитывая,
что ω = 2πf, получим
и
поскольку T = 1/f, где T — период колебаний,
то
Эти
формулы показывают, что период и частота
не зависят от амплитуды и начальной
фазы движения.
Модель
математического маятника.Математиический
маятник — осциллятор, представляющий
собой механическую систему, состоящую
из материальной точки, находящейся на
невесомой нерастяжимой нити или на
невесомом стержне в однородном поле
сил тяготения. Период малых собственных
колебаний математического маятника
длины l неподвижно подвешенного в
однородном поле тяжести с ускорением
свободного падения g равен
и
не зависит от амплитуды и массы
маятника.Плоский математический маятник
со стержнем — система с одной степенью
свободы. Если же стержень заменить на
растяжимую нить, то это система с двумя
степенями свободы со связью. Пример
школьной задачи, в которой важен переход
от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
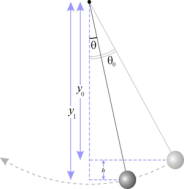Уравнение
колебаний маятника
Колебания
математического маятника описываются
обыкновенным дифференциальным уравнением
вида
где ω ― положительная константа,
определяемая исключительно из параметров
маятника. Неизвестная функция x(t) - это
угол отклонения маятника в момент t от
нижнего положения равновесия, выраженный
в радианах;
,
где L ― длина подвеса, g ― ускорение
свободного падения. Уравнение малых
колебаний маятника около нижнего
положения равновесия (т. н. гармоническое
уравнение) имеет вид:
.
Решения уравнения движения.
Гармонические колебания
Маятник,
совершающий малые колебания, движется
по синусоиде. Поскольку уравнение
движения является обыкновенным ДУ
второго порядка, для определения закона
движения маятника необходимо задать
два начальных условия — координату и
скорость, из которых определяются две
независимых константы:
где A — амплитуда колебаний маятника,
θ0 — начальная фаза колебаний, ω —
циклическая частота, которая определяется
из уравнения движения. Движение,
совершаемое маятником, называется
гармоническими колебаниями.
Нелинейный маятник
Для
маятника, совершающего колебания с
большой амплитудой, закон движения
более сложен:
где — это синус Якоби. Для
он является периодической функцией,
при малых совпадает с обычным
тригонометрическим синусом.
Параметр
определяется выражением
где
— энергия маятника в единицах
t-2Период
колебаний нелинейного маятника
где
K — эллиптический интеграл первого
рода.