22.Уравнение Колмогорова

23.Предельные вероятности состояний

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности состояний системы p_i при t →∞, т.е. в предельном стационарном режиме. В этом случае получают предельные (или финальные) вероятности состояний. В теории случайных марковских процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют. Существование предельных вероятностей означает, что с течением времени в системе наступает стационарный режим: она случайным образом меняет свои состояния, но вероятность p_i каждого из них уже не зависит от времени.

Предельная вероятность состояния p_i имеет чёткий смысл – это среднее относительное время пребывания системы в состоянии S_i (сколько процентов времени система проводит в состоянии S_i.). Например, если предельная вероятность состояния S_{0 ,} т.е. p₀₌ 0,5, то это означает, что в среднем половину времени система находится в состоянии S₀.

Так как предельные вероятности p_i постоянные, т.е. не зависят от времени, то , и в левой части уравнений Колмогорова получаем 0. Для решения этой системы удобно отрицательные слагаемые перенести из правой части исходной системы в левую часть. Для системы S с графом состояния § 2.4.1 (рис. 5), получим

стационарные уравнения Колмогорова

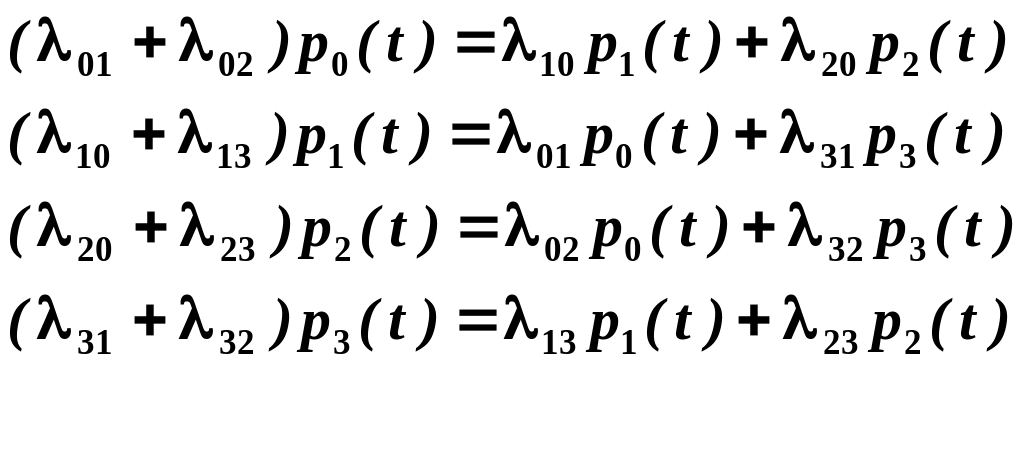(2.1.9)

Систему (2.1.9) можно составлять непосредственно по размеченному графу состояний, если руководствоваться следующим правилом.

При составления i-го уравнения системы уравнений Колмогорова для предельных вероятностей нужно рассмотреть состояние S_i на размеченном графе состояний. В левой части уравнения записывается сумма интенсивностей всех выходящих из S_i стрелок (потоков), умноженная на предельную вероятность p_i. Каждой входящей в S_i из S_j стрелке (на ней указана интенсивность λ_ji) в правой части уравнения соответствует слагаемое λ_ji p_i. В полученной системе уравнений одно уравнение будет выражаться через другие, т.к. они линейно зависимы. Поэтому какое-то одно уравнение этой системы нужно заменить уравнением

24. Одноканальная смо с отказами

Простейшей одноканальной моделью свероятностными входным потоком и процедурой обслуживания является модель, характери­зуемая показательным распределением как длительностей интерва­лов между поступлениями требований, так и длительностей обслу­живания. При этом плотность распределения длительностей интер­валов между поступлениями требований имеет вид где λ — интенсивность поступления заявок в систему (среднее число заявок, поступающих в систему за единицу времени). Плотность распределения длительностей обслуживания: , где – интенсивность обслуживания, t_об – среднее время обслуживания одного клиента. Пусть система работает с отказами. Можно определить абсолютную и относительную пропускную способность системы. Относительная пропускная способность равна доли обслуженных заявок относительно всех поступающих и вычисляется по формуле: . Эта величина равна вероятности Р₀ того, что канал обслуживания свободен. Абсолютная пропускная способность (А) — среднее число заявок, которое может обслужить система массового обслуживания в единицу времени: . Вероятность отказа в обслуживании заявки будет равна вероятности состояния «канал обслуживания занят»: . Данная величина Р_отк может быть интерпретирована как средняя доля необслуженных заявок среди поданных. Пример. Пусть одноканальная СМО с отказами представляет собой один пост ежедневного обслуживания для мойки автомобилей. Заявка — автомобиль, прибывший в момент, когда пост занят, — получает отказ в обслуживании. Интенсивность потока автомобилей λ 1,0 (автомобиль в час). Средняя продолжительность обслуживания — t_об=1,8 часа. Требуется определить в установившемся режиме предельные значения: относительной пропускной способности q; абсолютной пропускной способностиА; вероятности отказа Р_отк; Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый автомобиль обслуживался точно 1,8 часа и автомобили следовали один за другим без перерыва. Решение Определим интенсивность потока обслуживания: . Вычислим относительную пропускную способность: q = . Величина q означает, что в установившемся режиме система будет обслуживать примерно 35% прибывающих на пост автомобилей. Абсолютную пропускную способность определим по формуле: А=λ×q=1×0,356=0,356. Это означает, что система способна осуществить в среднем 0,356 обслуживания автомобилей в час. Вероятность отказа: Р_отк=1-q=1-0,356=0,644. Это означает, что около 65% прибывших автомобилей на пост ЕО получат отказ в обслуживании. Определим номинальную пропускную способность системы: А_ном= (автомобилей в час). Оказывается, что А_номв раза больше, чем фактическая пропускная способность, вычисленная с учетом случайного характера потока заявок и времени обслуживания.