19.Связь между поверхностными интегралами первого и второго родов.

 Отметим здесь лишь сам факт существования такой взаимной зависимости.

Пусть поверхность S задана уравнением: z = f(x,y), причем f(x,y), f'_x(x,y), f'_y(x,y) - непрерывные функции в замкнутой области τ (проекции поверхности S на координатную плоскость Оху), а функция R(x,y,z) непрерывна на поверхности S.

Нормаль к поверхности S, имеющая направляющие косинусы cosα, cosβ, cosγ, выбрана к верхней стороне поверхности S. Тогда

Для общего случая имеем:

*********************************

20.Вычисление потока векторного поля через замкнутую поверхность. Теорема Остроградского-Гаусса.

 Пусть задано векторное поле

Определение

 Дивергенцией или расходимостью векторного поля называется скалярная функция, определяемая равенством:
На этот раз векторное поле порождает скалярное поле .

С учетом понятий дивергенции и потока векторного поля формулу Остроградского можно представить в форме:

т. е. поток векторного поля через замкнутую поверхность S в направлении внешней нормали равен тройному интегралу от дивергенции векторного поля по области, ограниченной этой поверхностью.

На основании формулы (3.38) можно записать: и, переходя к пределу, стягивая V в точку М (при этом величина V 0 ), имеем:

То есть есть предел отношения потока поля через бесконечно малую замкнутую поверхность, окружающую точку М, к величине объёма, ограниченного этой поверхностью. Из этого следует, что дивергенция не зависит от выбора системы координат.

Если поток , то в область V втекает большее количество жидкости (если следовать ранее рассмотренному примеру о течении несжимаемой жидкости), чем вытекает из неё, т.е. внутри области V имеются источники жидкости.

Если П < 0, то внутри области V есть стоки.

Но поток векторного поля характеризует интенсивность источников и стоков лишь суммарно, т. е. при П ≥ 0 внутри области V могут быть как источники, так и стоки.

Для характеристики точки можно использовать   .

Если > 0, то данная точка есть источник,если < 0 - то сток.

Заметим, что можно записать с помощью символического вектора Гамильтона   в следующем виде: 

Отметим свойства дивергенции (справедливость которых рекомендуется показать самостоятельно):

 

*********************************

21.Криволинейный интеграл первого рода, его свойства.

 Пусть АВ - дуга гладкой кривой (рис. 3.1), на которой определена и непрерывна скалярная функция

f (x, y, z).

Выполним следующие действия:

1) разобьем дугу АВ произвольным образом на n частичных дуг ΔS₁, ΔS₂, ..., ΔS_i, ..., ΔS_n.

Через λ_n обозначим длину наибольшей из этих частичных дуг.

Понятно, что при λ_n → 0 автоматически n → ∞;

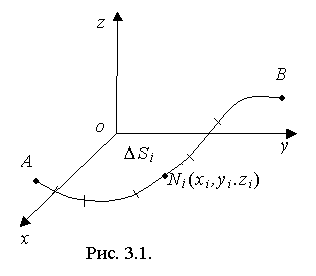
2) выберем произвольным образом точки ;

3)составим интегральную сумму вида , здесь под ΔS_i понимаем длины частичных дуг.

Определение

 

Конечный предел интегральной суммы α_n при λ_n → 0, если он существует и не зависит от способа деления дуги АВ на частичные дуги ΔS_i(i=1,...,n) и от способа выбора точек N_i(x_i,y_i,z_i) ΔS_i(i=1,...,n) называется криволинейным интегралом первого рода (по длине дуги) от функции f(x,y,z) по дуге АВ и обозначается

Имеются самые различные истолкования криволинейного интеграла по длине дуги, как геометрические, так и физические.

Например:

1) при - длина дуги АВ;

2) если функцию f(x,y,z) интерпретировать как плотность распределения вещества вдоль дуги АВ, то - масса дуги АВ.

Из определения криволинейного интеграла следует, что его величина не зависит от направления обхода дуги АВ, т.е.

Отметим условия существования интеграла (3.1).

Теорема

Если дуга АВ гладкая и функция f(x,y,z) непрерывна на ней, то интеграл (3.1) существует.

Можно сформулировать и значительно более сильную теорему об условиях существования интеграла (3.1).

********************