15.Поверхностный интеграл первого рода, его свойства.

Поверхностный интеграл первого рода является таким же обобщением двойного интеграла, как криволинейный интеграл первого рода по отношению к определённому интегралу.

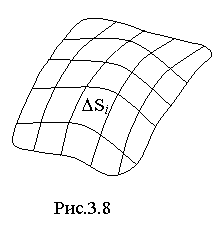
Пусть S - поверхность в трёхмерном пространстве Oxyz, а F(x,y,z) - непрерывная функция, определённая в точках этой поверхности. Поверхность S сетью линий разобьём на n участков ΔS₁, ΔS₂, ...., ΔS_i, ..., ΔS_n, не имеющих общих внутренних точек (рис. 3.8).

Площади "элементарных" участков обозначим теми же буквами S_i(i = 1,...,n), а наибольший из диаметров этих участков - через λ. На каждом "элементарном" участке ΔS_i произвольным образом выберем по точке M_i(x_i,y_i,z_i) (i = 1,...,n) и составим сумму которая называется интегральной суммой для функции F(x,y,z) по поверхности S.

Определение

Если существует конечный предел , не зависящий от способа разбиения поверхности S на "элементарные" участки ΔS_i и от выбора точек M_i ΔS_i(i=1,....n), то он называется поверхностным интегралом первого рода от функции f(x,y,z) по поверхности S и обозначается
Поверхностный интеграл обладает всеми обычными свойствами интеграла, включая теорему о среднем значении.

Приведём простейшие достаточные условия существования поверхностного интеграла первого рода.

Теорема

Если поверхность S задана уравнением z = f(x,y), где функция f(x,y) и её частные производные f'_x(x,y) и f'_y(x,y) непрерывны в замкнутой области τ (τ - есть область, в которую проектируется поверхность S на координатную плоскость Oху), а функция F(x,y,z) непрерывна на S, то интеграл существует. К использованию этих условий, равно как и условий, получающихся из них перестановкой переменных x, y, z сводится большинство практически встречающихся случаев.

16.Методы вычисления поверхностного интеграла первого рода.

Вычисление поверхностных интегралов первого рода обычно производится путём их сведения к двойным интегралам.

Пусть выполнены все условия приведенной выше теоремы, тогда, обозначив проекцию ΔS_i (и площадь проекции) на плоскость Oxy через Δτ_i, по теореме о среднем значении будем иметь: где (x_i, y_i) Δτ_i, а, следовательно, при данном специфическом выборе точек M_i.

Но сумма, стоящая справа, в последнем интеграле есть интегральная сумма для функции по плоской области τ. Переходя к пределу, получаем: Если проектировать поверхность S не на координатную плоскость Oxy, а на координатную плоскость Oxz или Oyz, то можно записать формулы для вычисления поверхностного интеграла аналогично формуле (3.14).

Приложения поверхностного интеграла различны. Так, например:

1) если положить F(x,y,z)=1, то интеграл (3.12) будет численно равен площади поверхности S. 2) если же функцию F(x,y,z) интерпретировать как плотность вещества, распределенного по поверхности S, то интеграл (3.12) численно равен массе материальной поверхности S.

*********************************

17.Поток векторного поля, его гидродинамический смысл.

Понятие потока векторного поля удобно рассматривать на примере потока жидкости, движущейся через некоторую поверхность. Объем жидкости, протекающей в единицу времени через поверхность, расположенную в движущейся жидкости, назовем потоком жидкости через эту поверхность.

Пусть поверхность S расположена в поле скоростей частиц несжимаемой жидкости с плотностью ρ=1.

Можно показать, что поток векторного поля в этом случае равен где - единичный нормальный вектор к поверхности S, расположенный по одну сторону с вектором , а величина . Независимо от физического смысла вектора , интеграл (3.34) по поверхности называют потоком векторного поля через поверхность S. Пусть и , тогда поток П вектора через поверхность S можно записать в виде: 

Или учитывая связь поверхностных интегралов первого и второго родов, можно записать поток П через поверхностный интеграл в координатах: