
- •Сжатие информации Оглавление
- •1. Виды информации
- •2. Количество информации.
- •3. Хранение, измерение, обработка и передача информации
- •4. Базовые понятия теории информации
- •5. Обзор подходов к сжатию информации
- •6. Эффективное посимвольное кодирование для сжатия данных.
- •Сжатие информации с учетом цепочек символов по Лемпелю-Зиву (Велчу).
- •8. Сжатие изображений по блочному алгоритму jpeg.
- •9. Методы сжатия звуковой информации
6. Эффективное посимвольное кодирование для сжатия данных.
Напомним, что об эффективном кодировании уже шла речь в подразделе 5. Основные моменты сводятся к следующему:
идея такого кодирования базируется на том, чтобы использовать для часто встречающихся символов более короткие кодовые цепочки, а для редких - более длинные. В результате средняя длина кода
 будет меньше, чем при равномерном
кодировании;
будет меньше, чем при равномерном
кодировании;согласно теореме Шеннона, наилучшее кодирование позволяет сократить lср. до величены энтропии Н, подсчитанной для данного набора символов;
добавим, что неравномерное кодирование позволяет автоматически устранить избыточность, связанную с тем, что количество символов в алфавите может быть не кратно степени двойки (так, например, чтобы закодировать одинаковым числом разрядов 5 разновидностей символов потребуется 3 бита, так же как и для 8 символов).
Идея неравномерного кодирования, в котором длина кодовой цепочки зависит от частоты появления соответствующего символа, реализована еще в знаменитой «азбуке Морзе». Однако там наряду с «точками» и «тире» использовался третий кодовый символ – разделитель «пауза». Если ограничиться только «O» и «1», то при построении кода необходимо учесть дополнительное требование: чтобы все кодовые цепочки однозначно выделялись в непрерывном потоке битов, ни одна из них не должна входить как начальный участок в кодовую, цепочку другого символа. Такое свойство кода называется префиксностью.
Наибольшее распространение получил способ построения эффективного кода предположенный Хаффманом. Рассмотрим его на примере. Пусть задан алфавит из 5 разновидностей символов Z1 – Z5, и их вероятности. В таблице 6.1 наряду с этими исходными данными приведены так же результаты кодирования по Хаффману: кодовые цепочки Ki их длинны li. Процедуру построения кода иллюстрирует таблица 6.2 и рисунок 5
Пример кода Хаффмана
Таблица 6.1
Zi |
Pi |
Ki |
li |
Z1 Z2 Z3 Z4 Z5 |
0,25 0,17 0,08 0,35 0,15 |
10 00 010 11 011 |
2 2 3 2 3 |
|
|
|
lср |
Объединение вероятностей символов
Таблица 6.2
Zi |
Pi |
Шаги объединения |
Ki |
|||
1 |
2 |
3 |
4 |
|||
Z1 Z2 Z3 Z4 Z5 |
0,35 0 0,17 0 0,08 |
0 0,25 0 0,17 |
0 0 ,35 0,25 |
0 0,40 |
1,00 |
11 10 00 011 010 |
На первом этапе символы упорядочивают по убыванию вероятностей, а затем выполняют несколько шагов «объединения», на каждом из которых суммируются вероятности наиболее редко встречающихся символов и столбец вероятностей пересортировывается (см. табл.6.2).
На втором этапе строится «дерево кода», ветви которого отображают в обратном порядке процесс «объединения вероятностей». При построении дерева принимается правило соответствия большей вероятности одному из направлений ветви (например «левому») и определенному значению бита кода (например, «1») (рис.5). Цепочки битов от «корня» до конца каждой ветви соответствуют кодам исходных символов (табл.6.1 – 6.2).
|
В табл.6.2 наглядно видны следующие закономерности кода:
- часто встречающиеся символы получили более короткие кодовые цепочки. В частности, за счет этого средняя длина цепочки составила lср = 2,23, что значительно меньше, чем lср = 3,00 при равномерном кодировании;
- ни одна из цепочек не входит как начальный участок в другую (выполняется так называемое правило «префиксности», благодаря чему коды символов легко можно выделить в потоке битов.
|
Рис.5 «Дерево кода» по Хаффману
Процедура кодирования сводится к выбору из кодовой таблицы цепочек, соответствующих каждому символу источника. Декодирование предусматривает выделение в битовом потоке кодов символов и их расшифровку в соответствии с таблицей. Пример показан на рис.6.
Передаваемые символы Z1, Z2, Z3, Z4 , Z5
Битовая последовательность 00 11 10 011 111
Принятые символы Z1*, Z2*, Z3*, Z4* , Z5*
(результат декодирования)
Рис.6 Пример кодирования и декодирования по Хаффмену
Код Хаффмена может быть двухпроходным и однопроходным. Первый строится по результатам подсчета частот (вероятностей) появления различных символов в данном сообщении. Второй использует готовую таблицу кодирования, построенную на основе вероятностей символов в сообщениях похожего типа. Например, кодирование текста на русском языке в первом случае включает его предварительный анализ, подсчет вероятностей символов, построение дерева кода и таблицы кодирования индивидуально для данного сообщения. Во втором случае будет работать готовая таблица, построенная по результатам анализа множества русскоязычных текстов. Двухпроходный код более полно использует возможности сжатия. Однако, при этом вместе с сообщением нужно передавать и кодовую таблицу. Однопроходный код не оптимален, однако прост в использовании, поэтому на практике обычно применяют именно его.
В целом код Хаффмена проигрывает по сравнению с «цепочечными» кодами и его редко используют самостоятельно, однако он часто фигурирует как элемент более сложных алгоритмов сжатия.

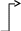 ,25
,25 ,15
,15 ,35
,35 ,23
,23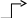 ,40
,40
 ,60
,60