
- •Ответы по дисциплине «Основы алгоритмизации и программирования»
- •Запись алгоритма Евклида на языке с
- •Int main() {
- •Эвристический алгоритм «ближайшего соседа»
- •Эвристический алгоритм «ближайших пар»
- •«Правильный» алгоритм поиска маршрута
- •Эволюция языка с bcpl → b → c → k&r c → ansi c → c99 → c1x
- •#Define имя текст_для_подстановки
- •123, 67543, 037, 07777, 0Xabf7, 0xffff, …
- •123456789L, 0xful (это просто число 15).
- •Определение символических констант в limits.H
- •Int lower, upper, step;
- •Int main() {
- •Int main() {
- •Int main() {
- •Всего операций: 47
- •If (условие) оператор
- •If (условие) оператор1 else оператор2
- •Int main() {
- •Int main() {
- •Int main() {
- •Int main() {
- •If (found)
- •Адресация памяти
- •Адреса объектов программы
- •Int fact(int n) {
- •О размерах участков памяти, выделяемых объектам
- •Правила адресной арифметики
- •Никакие другие операции к адресам неприменимы, т.Е. Адреса нельзя умножать, делить, складывать между собой и пр.
- •Имя массива – это константный указатель на его начало.
- •T X[] эквивалентно t *X
- •Int main() {
- •Void *calloc(size_t n, size_t r)
- •Void free(void *p)
- •Int main() {
- •Void *p;
- •Void swaps(char** a, char** b) {
- •Int main(void) {
- •Int main() {
- •Правило «право-лево»
- •Int pt_in_rect(struct point p, struct rect r) {
- •Int main() {
- •Int main() {
- •Int ival;
- •Void init(Vector*);
- •Void resize(Vector*, int);
- •Void push_back(Vector*, double);
- •Void push_s(Stack *st, double d) {
- •Void init_q(Queue *q) {
- •Void enqueue(Queue *q, double d) {
- •Int dequeue(Queue *q, double *d) {
- •Typedef struct Heap {Vector V;} Heap;
- •Void init_h(Heap *hp) {
- •Int Heap_Maximum(Heap *hp, double *z) {
- •Void Max_Heap_Insert(Heap *hp, double X){
- •Void Max_Heapify(Heap *hp, int I) {
- •Int l, r, largest;
- •Int Heap_Extract_Max(Heap *hp, double *z) {
- •Void Build_Max_Heap(Heap *hp) {
- •Void Insert_head_l1(List1 *l, double z) {
- •Void Insert_back_l1(List1 *l, double z) {
- •Int Extract_head_l1(List1 *l, double *z) {
- •Int Extract_back_l1(List1 *l, double *z) {
- •Void reverse_l1(List1 *l) {
- •Исходный код функции sort_l1
- •Void sort_l1(List1 *l) {
- •Void visit(List1* l) {
- •Void traverse(List1* l) {
- •Void Print_l1(List1 *l) {
- •Void Insert_l2(List2 *l, double z, int direction) {
- •Прямой обход (сверху вниз), при котором мы посещаем узел, а затем левое и правое поддеревья
- •Поперечный обход (слева направо), при котором мы посещаем левое поддерево, затем узел, а затем правое поддерево
- •Обратный обход (снизу вверх), при котором мы посещаем левое и правое поддеревья, а затем узел.
- •Простой метод сортировки массива
- •Задача о взвешивании монет
- •1) Очевидно, что на последнем шаге процедуры взвешивания мы должны иметь дело максимум с 3 монетами, чтобы в при любом исходе взвешивания получить результат.
- •2) Задача предпоследнего шага – отобрать группу из 3-х монет. Это можно сделать, если в нашем распоряжении будет не более 9 монет (3 группы по 3 монеты).
- •3) Наконец, если у нас будет от 10 до 27 монет, мы сможем отобрать из них не более 9
- •Void mov(int n, char a, char c, char b) {
- •Int main() {
Прямой обход (сверху вниз), при котором мы посещаем узел, а затем левое и правое поддеревья
Поперечный обход (слева направо), при котором мы посещаем левое поддерево, затем узел, а затем правое поддерево
Обратный обход (снизу вверх), при котором мы посещаем левое и правое поддеревья, а затем узел.
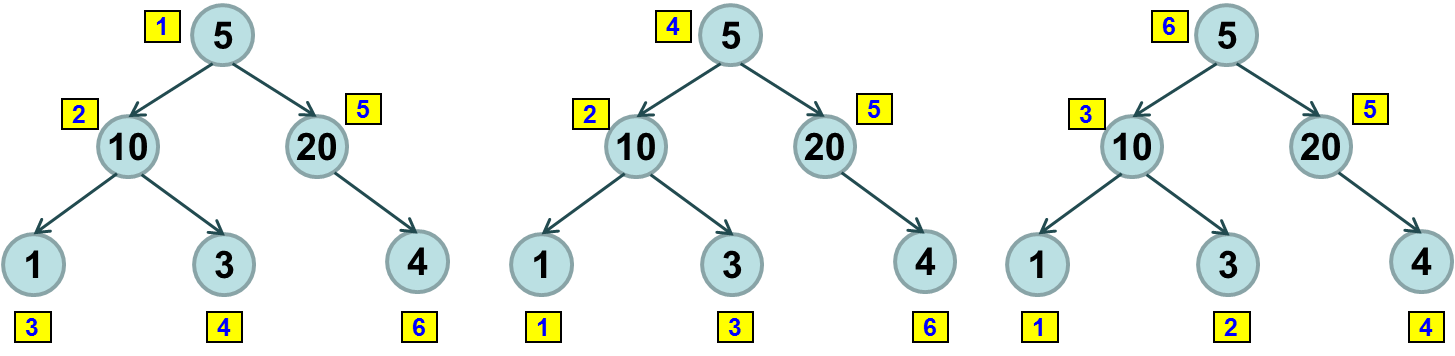
Вопрос №96. Алгоритмы обхода бинарного дерева.
Для решения многих задач можно непосредственно применять рекурсивные алгоритмы типа «разделяй и властвуй», которые, по существу, обобщают алгоритмы обхода деревьев:
Обработка дерева выполняется посредством обработки корневого узла и (рекурсивно) его поддеревьев; вычисление можно выполнять перед, между или после рекурсивных вызовов (или же использовать все три метода).
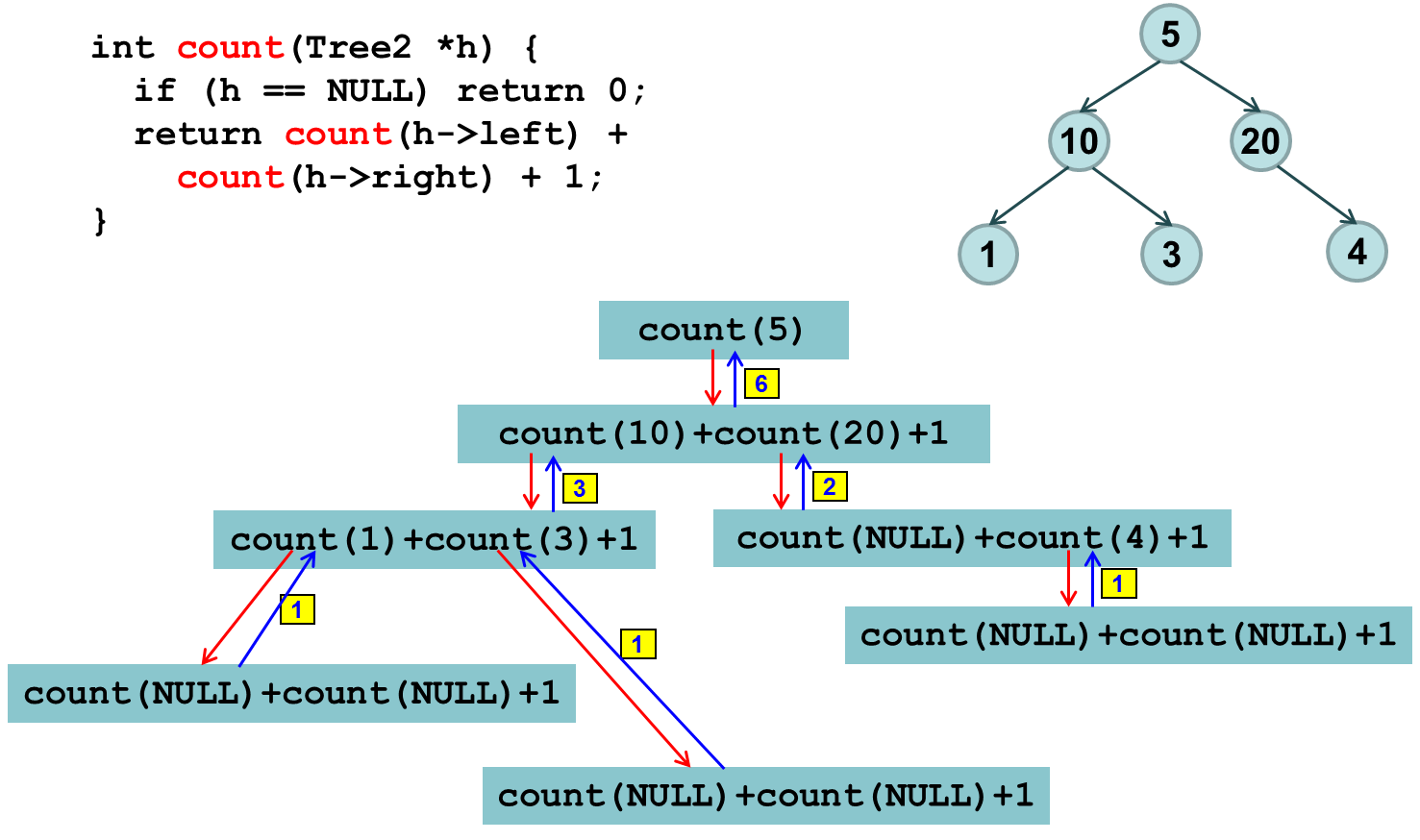
Вопрос №97. Алгоритм вычисления высоты бинарного дерева.
Для решения многих задач можно непосредственно применять рекурсивные алгоритмы типа «разделяй и властвуй», которые, по существу, обобщают алгоритмы обхода деревьев:
Обработка дерева выполняется посредством обработки корневого узла и (рекурсивно) его поддеревьев; вычисление можно выполнять перед, между или после рекурсивных вызовов (или же использовать все три метода).

Лекция 18. Корневые деревья (продолжение).
Вопрос №98. Корневые деревья с произвольным ветвлением (сильноветвящиеся деревья): основные характеристики и внутреннее устройство. Эффективный способ представления сильноветвящихся деревьев.
До сих пор мы рассматривали только способы представления бинарных деревьев. В ряде задач используются сильноветвящиеся деревья, у которых любой узел может иметь произвольное количество дочерних узлов. Пример – файловая система.
Схему представления бинарных деревьев можно обобщить и для сильноветвящихся деревьев, в которых количество дочерних узлов не превышает некоторой константы K. При этом поля с указателями left и right заменяются полями child1, child2, … childK. Если количество дочерних элементов узла не ограничено, то такой подход не работает, поскольку заранее не известно, для какого количества указателей нужно выделить место. Кроме того, если количество дочерних элементов K ограничено большой константой, но на самом деле у многих узлов потомков намного меньше, то значительный объем памяти будет израсходован напрасно.
Однако существует эффективный способ представления деревьев с произвольным количеством дочерних узлов с помощью бинарных деревьев. Такой способ называется представлением с «левым дочерним и правым сестринским узлами» (left-child, right-sibling representation).
Как и в представлении бинарного дерева, в каждом узле такого представления дерева содержатся 3 указателя:
указатель р для ссылки вверх на «родительский» узел,
указатель lchild для ссылки влево-вниз на крайний левый дочерний узел,
указатель sibling для ссылки вправо на «родную сестру (брата).
typedef struct TreeN {
char elem;
struct TreeN *p, *lchild, *sibling; } TreeN;
На рисунках ниже представлено обычное изображение дерева и изображение с помощью представления с «левым дочерним и правым сестринским узлами».
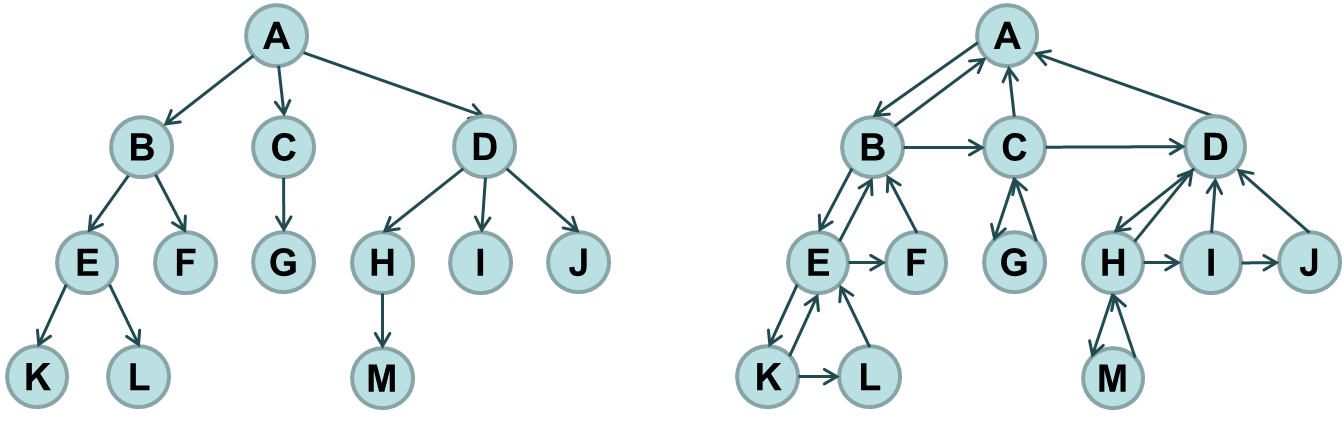
Вопрос №99. Алгоритм обхода сильноветвящегося дерева.
Можно провести определенную аналогию между обходом бинарного дерева и обходом сильноветвящегося дерева и предложить две стратегии такого обхода:
Прямой обход (сверху вниз), при котором мы сначала посещаем узел, а затем все его поддеревья,
Обратный обход (снизу вверх), при котором мы сначала посещаем все поддеревья узла, а затем сам узел.
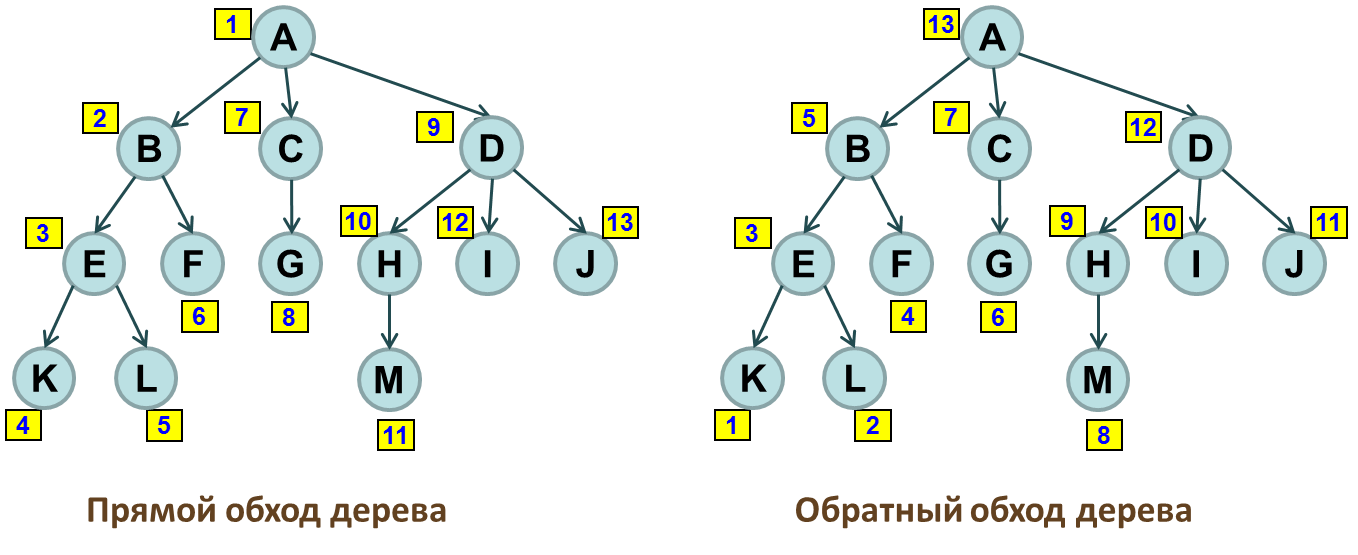
Ниже представлены тексты рекурсивных функций preorder и postorder, которые в каждом посещенном узле дерева вызывают функцию visit для выполнения некоторой «полезной работы» (например, для печати содержимого узла). Первая из них сначала вызывает visit, а затем проходит по всем дочерним узлам, а вторая – наоборот, сначала проходит по дочерним узлам, а затем вызывает visit.
void visit(TreeN* h) {
printf("%c ", h->elem);
}
void preorder(TreeN* h) {
if (h == NULL) return;
TreeN* p;
visit(h);
for(p = h->lchild; p != NULL; p = p->sibling) preorder(p);
}
void postorder(TreeN* h) {
if (h == NULL) return;
TreeN* p;
for(p = h->lchild; p != NULL; p = p->sibling) postorder(p);
visit(h);
}
Лекция 19. Методы разработки алгоритмов.
Вопрос №100. Разработка алгоритмов методом частных целей (на примере простого алгоритма сортировки).
Первый метод связан со сведением трудной задачи к последовательности более простых задач. Конечно, мы надеемся на то, что более простые задачи легче поддаются обработке, чем первоначальная задача, а также на то, что решение первоначальной задачи может быть получено из решений этих более простых задач. Такая процедура называется методом частных целей.
Этот метод выглядит очень разумно. Но, как и большинство общих методов решения задач или разработки алгоритмов, его не всегда легко перенести на конкретную задачу. Осмысленный выбор более простых задач— скорее дело искусства или интуиции, чем науки. Более того, не существует общего набора правил для определения класса задач, которые можно решить с помощью такого подхода. Размышление над любой конкретной задачей начинается с постановки вопросов. Частные цели могут быть установлены, когда мы получим ответы на следующие вопросы:
1. Можем ли мы решить часть задачи? Можно ли, игнорируя некоторые условия, решить оставшуюся часть задачи?
2. Можем ли мы решить задачу для частных случаев? Можно ли разработать алгоритм, который дает решение, удовлетворяющее всем условиям задачи, но входные данные которого ограничены некоторым подмножеством всех входных данных?
3. Есть ли что-то, относящееся к задаче, что мы не достаточно хорошо поняли? Если попытаться глубже вникнуть в некоторые особенности задачи, сможем ли мы что-то узнать, что поможет нам подойти к решению?
4. Встречались ли мы с похожей задачей, решение которой известно? Можно ли видоизменить ее решение для решения нашей задачи? Возможно ли, что эта задача эквивалентна известной нерешенной задаче?
