Int Heap_Extract_Max(Heap *hp, double *z) {
if(hp->v.sz == 0) return 0; // если пирамида пуста - выход
*z = hp->v.elem[0];
hp->v.elem[0] = hp->v.elem[--(hp->v.sz)];
Max_Heapify(hp, 0); // спуск элемента, находящегося в корне
return 1;
}
Вопрос №80. Алгоритм преобразования массива в пирамиду.
Решим следующую задачу: заданный массив преобразовать в пирамиду. Пусть задан массив чисел: {1,2,3,4,7,8,9,10,14,16}. Изобразим его в форме пирамиды:
Очевидно,
что полученная пирамида неправильная
и её нужно исправить. Начнем процедуру
исправления с первого узла, у которого
есть потомки (это узел номер 4) и в каждом
цикле будем уменьшать этот номер на 1.
Т.о. исправлению подлежат поддеревья с
вершинами 4,3,2,1,0.
На рисунке ниже показан результат исправления для вершин 4, 3 и 2:
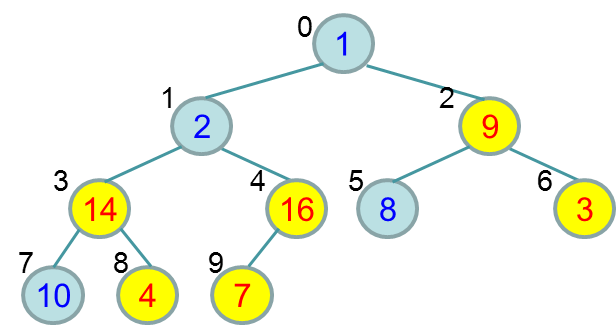
Исправление вершины 1 потребовало двух ходов:
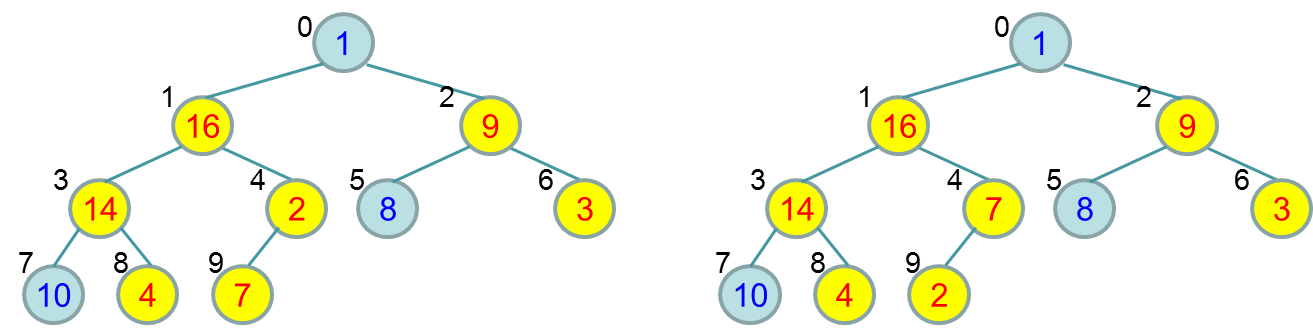
Исправление вершины 0 потребует уже трёх ходов (второй ход пропущен):
Описанный выше алгоритм представлен ниже в виде функции Build_Max_Heap:
Void Build_Max_Heap(Heap *hp) {
int i;
for(i=(hp->v.sz-1)/2; i >= 0; i--) Max_Heapify(hp, i);
}
Теперь можно приступить к конструированию модульной структуры приложения, использующего абстракцию «пирамида». Прежде всего, сформируем интерфейс, в который поместим описание структуры Heap, а также описания клиентских функций для работы с пирамидами: init_h, Heap_Maximum, Max_Heap_Insert, Max_Heapify, Heap_Extract_Max и Build_Max_Heap.
Как отмечалось ранее, интерфейс помещается в заголовочный файл, который назовем Heap.h :
// Vector.h
typedef struct Heap {Vector v;} Heap;
void init_h(Heap*);
int Heap_Maximum(Heap*, double*);
void Max_Heap_Insert(Heap*, double);
void Max_Heapify(Heap*, int);
int Heap_Extract_Max(Heap*, double*);
void Build_Max_Heap(Heap*);
Вопрос №81. Структура данных «очередь с приоритетом».
Пирамида является очень эффективным средством для реализации очереди с приоритетом – особого вида очереди, в которой в «голове очереди» всегда расположен элемент с максимальным значением ключа (т.е. имеющий максимальный приоритет). Именно этот элемент и будет первым извлекаться из очереди и направляться на обслуживание.
Одна из областей применения очередей с приоритетом— планирование заданий на компьютере, который совместно используется несколькими пользователями. Очередь позволяет следить за заданиями, которые подлежат выполнению, и за их приоритетами. Если задание прервано или завершило свою работу, из очереди с помощью операции Heap_Extract_Max выбирается следующее задание с наибольшим приоритетом. В очередь в любое время можно добавить новое задание, воспользовавшись операцией Max_Heap_Insert.
Связанные списки
Вопрос №82. Однократно связанный (однонаправленный) список: основные характеристики и внутреннее устройство.
Связанный список (linked list) — это структура данных, элементы которой расположены в линейном порядке. Однако, в отличие от массива, в котором этот порядок определяется индексами, порядок в связанном списке поддерживается с помощью указателей. Связанные списки обеспечивают простое и гибкое представление динамических множеств и поддерживают все операции, рассмотренные ранее для массивов.
Списки могут быть разных видов. Простейшим из списков является однократно связанный (однонаправленный - singly linked) список. Будем обозначать вид таких списков L1.
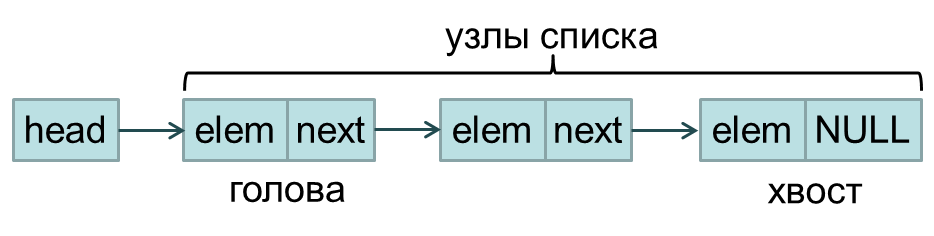
typedef struct Node1 {
double elem; struct Node1 *next; } Node1;
typedef struct List1 { Node1* head; } List1;
Ниже приведена иллюстрация пустого однонаправленного списка и текст функции init_L1 , инициализирующей такой список.
Вопрос №83. Алгоритм включения элемента в однонаправленный список.
Задача включения нового элемента в однонаправленный список может быть решена двумя способами:
включение в голове списка (перед первым элементом) или
включение в хвосте списка (после последнего элемента).
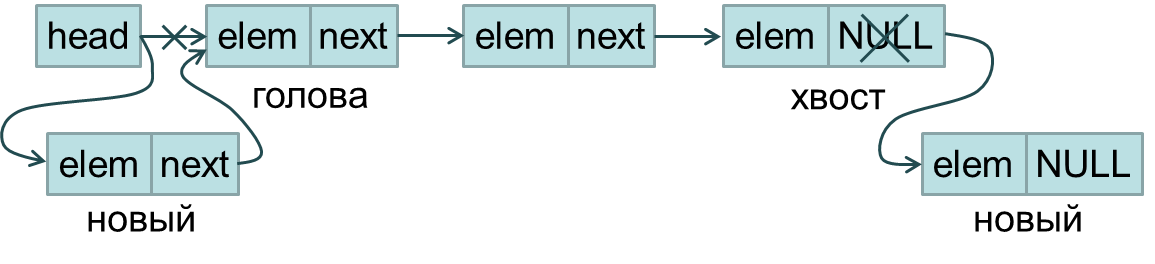
Тексты двух функций, реализующих включение нового элемента в голове списка Insert_head_L1 и в хвосте списка Insert_back_L1.