
- •11. Геометрическая оптика. Учет влияния дифракционных эффектов.
- •11.3. Описание лучевой картины для типичных случаев неоднородности.
- •12.4. Релятивистская механика частицы. 4 – скорость. 4 – ускорение. Четырехмерное уравнение движения. 4 – импульс. Сила Минковского. Энергия частицы. Принцип эквивалентности.
- •Таким образом, имеем две формы записи для 4 – вектора скорости частицы
- •Часть III. Электродинамика плазмы и газового разряда. Основы электрогидродинамики.
- •13. Основные понятия физики плазмы. Электродинамика быстрых процессов в плазме
- •13.2. Уравнения электродинамики быстропеременных процессов в плазме. Диэлектрическая проницаемость однородной изотропной плазмы.
- •14 Электродинамика медленных процессов в плазме. Ионно – звуковые волны. Магнитная гидродинамика.
- •14.7. Условия применимости уравнений мгд.
- •14.11.Относительная роль конвекции и диффузии.
- •14.13. Свойства равновесных статических мгд конфигураций.
- •14.14. Пинч - эффект.
- •15.5. Температура заряженных частиц.
- •15.9. Амбиполярная диффузия слабоионизированной плазмы. Рекомбинация. Положительный столб тлеющего разряда. Вольт - амперная характеристика (вах) разряда между электродами.
- •15.12. Положительный столб дугового стационарного разряда.
- •16. Основы электрогидродинамики.
- •16.2. Электрострикция в неоднородных средах.
16.2. Электрострикция в неоднородных средах.
Плотность
силы
![]() описывает эффект электрострикции в
неоднородной среде (воздействие силы
высокочастотного давления, за счет
неоднородности электрического поля и
за счет частичного учета влияния
неоднородности среды). Ниже будет
показано, что сила
описывает эффект электрострикции в
неоднородной среде (воздействие силы
высокочастотного давления, за счет
неоднородности электрического поля и
за счет частичного учета влияния
неоднородности среды). Ниже будет
показано, что сила
![]() так же будет учитывать влияние
неоднородности среды (В однородной
среде
так же будет учитывать влияние
неоднородности среды (В однородной
среде
![]() ).
).
Движение
ионой компоненты в однородной среде,
но в неоднородном электрическом поле
![]() (
- частота быстрых осцилляций) опишем
уравнением
(
- частота быстрых осцилляций) опишем
уравнением
![]() .
.
Чтобы
не загромождать описание, в правой части
уравнения выписан только один член.
Смещение ионов разобьем на две части:
![]() ,
где
,
где
![]() описывает медленные движения, а
описывает медленные движения, а
![]() характеризует быстрые движения.. При
этом рассматривается ситуация, когда
имеет место система неравенств
характеризует быстрые движения.. При
этом рассматривается ситуация, когда
имеет место система неравенств ![]() .
.
Будем
иметь описание быстрого процесса, когда
имеет место
![]()
![]() .
.![]() . (16.1)
. (16.1)
Описание медленного движения получается в результате усреднения по периоду высокочастотных колебаний уравнения :
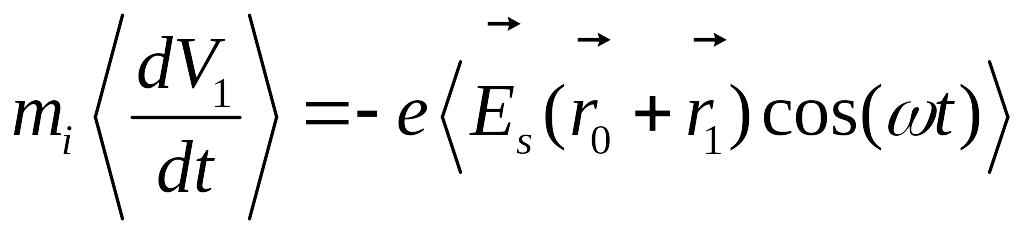 ,
,
где
учтено ![]() .
.
Учтем
возможность разложения в ряд Тейлора ![]()
Произведя
усреднение по периоду высокочастотных
колебаний, и учтя представление (16.1),
получим описание медленного движения
одного иона ![]()
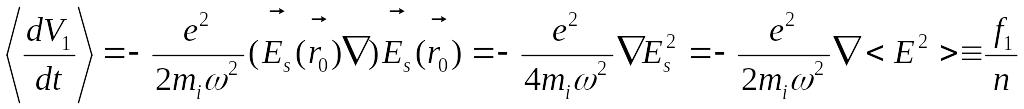 ,
,
где
учтено, что
![]() .
Таким образом, имеем представление для
плотности силы электрострикции в
однородной электропроводящей среде
при наличии неоднородного электрического
поля
.
Таким образом, имеем представление для
плотности силы электрострикции в
однородной электропроводящей среде
при наличии неоднородного электрического
поля ![]()
Впервые
описание электрострикции для случая
быстрых процессов в плазме было сделано
Миллером М.А. (1958 г.) (в такой ситуации
движение ионов пренебрежимо мало). В
формуле для
в этом случае следует сделать замену
![]() ,
соответствующая сила называется силой
Миллера.
,
соответствующая сила называется силой
Миллера.
Если
исходить из приближения ионных плазменных
колебаний, то
![]() ,
где
,
где
![]() ,(здесь
введено обозначение
,(здесь
введено обозначение
![]() ).
В результате получаем другую форму
описания силы электрострикции в случае
однородной среды для задач
электрогидродинамики
).
В результате получаем другую форму
описания силы электрострикции в случае
однородной среды для задач
электрогидродинамики ![]() .
.
В
неоднородной среде имеет место обобщение
этой формулы (вывод этой формулы делать
не будем) ![]() .
.
Сила электрострикции имеет потенциальный характер, она приводит к уменьшению давления (уменьшению концентрации заряженных частиц в области больших значений поля ).
Влияние
неоднородной среды приводит к возникновению
еще дополнительной нелинейной силы
![]() .
Приведем без обоснования ее представление
.
Приведем без обоснования ее представление ![]() .
.
16.3. Условия применимости уравнений ЭГД. Основным условием применимости уравнений ЭГД является допущение о пренебрежении влиянием магнитного поля:
![]() . (16.2)
. (16.2)
При
этом в законе Ома для медленных процессов
![]() сделаем пренебрежение вторым слагаемым
в правой части равенства. Это допустимо
делать при выполнении условия
сделаем пренебрежение вторым слагаемым
в правой части равенства. Это допустимо
делать при выполнении условия ![]() . (16.3)
. (16.3)
Из
уравнения Максвелла
![]() следует оценка магнитного поля
следует оценка магнитного поля
![]() , (16.4)
, (16.4)
где
характерный пространственный масштаб
изменения полей. В результате, на основе
(16.3), (16.4) получаем условие ![]() ,
,
где
![]() - магнитное число Рейнольдса,
- магнитное число Рейнольдса,
![]() - коэффициент магнитной вязкости. В
качестве примера возьмем параметры
- коэффициент магнитной вязкости. В
качестве примера возьмем параметры
![]() .
Получаем условие на скорость движения
среды
.
Получаем условие на скорость движения
среды
![]() .
.
Соотношение (16.2) при учете (16.3) приводят к условию
![]() ,
,
![]()
![]() ,
, ![]() ,
,
или к дополнительному ограничению на магнитное число Рейнольдса
![]() .
.
Рассмотрим
пример
![]() ,
в такой ситуации условие на электропроводность
принимает вид
,
в такой ситуации условие на электропроводность
принимает вид
![]() .
.
Уравнение Максвелла можно записать в другой, эквивалентной форме
![]() .
.
Сделаем
оценку на основе представления
![]() ,
справедливого для сред без дисперсии
в линейном приближении.
,
справедливого для сред без дисперсии
в линейном приближении. ![]() ,
,
где - характерное время изменения полей. С учетом (16.2) получаем неравенство
![]() . Для
рассмотренного выше примера имеем
. Для
рассмотренного выше примера имеем
![]()
16.4.
Невозмущенное состояние. Рассмотрим
статическое невозмущенное состояние
неподвижной среды (![]() ).
В таком случае создается неоднородное
состояние
).
В таком случае создается неоднородное
состояние
![]() ,
,
![]()
![]() ,
, ![]()
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Это
сложная нелинейная задача, описываемая
системой нелинейных дифференциальных
уравнений в частных производных с
переменными коэффициентами. В общем
случае такое состояние может быть
неустойчивым. Ситуация упрощается при
пренебрежении влиянием силы тяжести
![]() .
.
16.5.
Линейное приближение. Рассмотрим
систему уравнений, описывающую ЭГД
волны малой амплитуды в линейном
приближении. Считаем, что поля
представляются в виде
![]() ,
где
,
где
![]() и в системе уравнений ЭГД ограничимся
учетом членов первого порядка малости.
и в системе уравнений ЭГД ограничимся
учетом членов первого порядка малости.
![]()
![]() ,
,
![]() ,
,

 ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
В
зависимости от особенностей конкретных
ЭГД задач, в этой системе уравнений
делается учет не всех членов. В частности,
в ситуации
![]()
![]() система уравнений сильно упрощается и
распадается на две независимые системы,
описывающие волновой процесс в
электронейтральной среде и потенциальное
электрическое поле.
система уравнений сильно упрощается и
распадается на две независимые системы,
описывающие волновой процесс в
электронейтральной среде и потенциальное
электрическое поле.
16.6. Классификация ЭГД явлений. Удобную классификацию задач можно дать по силам, играющим основную роль в волновом процессе. Конечно, это можно сделать лишь в том случае, когда имеет место преобладание части сил.
В приближении идеального диэлектрика отсутствуют свободные заряды:
 ,
.
Такая идеализация допустима при
выполнении условия
,
.
Такая идеализация допустима при
выполнении условия
![]() ,
или
,
или
![]() ,
,
где - характерное время изменения полей.
Пренебрежение токами смещения по сравнению с токами проводимости в ситуации
![]() или
или
![]() .
.
Когда делается пренебрежение эффектом джоулева нагрева среды (по сравнению с проявлением явления теплопроводности), то возникает ограничение на величину электропроводности сверху:
![]() .
.
Круг задач, в которых проявляется сильное влияние неоднородности среды и неоднородности полей. Примером такой задачи является образование электрического ветра в резко неоднородных полях около тонких проволок и острых предметов.
