
- •Задания к контрольной работе (матанализ ч. 2) для заочников.
- •Тематический план.
- •Перечень заданий. Неопределенный интеграл функции одной переменной
- •Дифференциальное исчисление функции двух переменных
- •Геометрические приложения определенного интеграла
- •Примеры
- •Функции многих переменных Частные производные. Геометрическая интерпретация частной производной.
- •Теоремы о дифференцируемых фмп.
- •Экстремумы фмп.
- •Примеры
Примеры
Задача
№1: Найти частные производные для функции
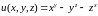 .
.
Решение:
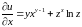 ,
,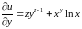 ,
,
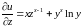 .
.
Задача
№2: Найти
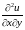 , если
, если
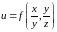 .
.
Решение:
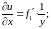
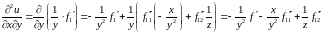 .
.
Задача №4:
Исследовать
на экстремумы функцию
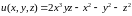 .
.
Решение:
Координаты
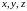 критической точки вследствие гладкости
функции должны удовлетворять системе
критической точки вследствие гладкости
функции должны удовлетворять системе
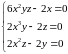 или
или
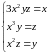
Из системы уравнений получим пять критических точек:
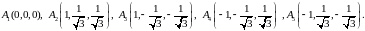
Так
как
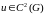 для любой области
для любой области
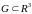 ,
то возможно дальнейшее исследование
поведения функции
,
то возможно дальнейшее исследование
поведения функции
 в стационарных точках с помощью
достаточного условия экстремума:
в стационарных точках с помощью
достаточного условия экстремума:
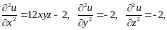
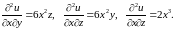
Отсюда
получим, что в точке
 :
:
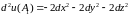 .
Так как этот является ни чем иным как
отрицательно определенной квадратичной
формой (5.11), то можно сделать вывод что
в точке
функция
имеет строгий локальный максимум.
.
Так как этот является ни чем иным как
отрицательно определенной квадратичной
формой (5.11), то можно сделать вывод что
в точке
функция
имеет строгий локальный максимум.
Рассмотрим
точку
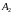 :
:
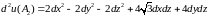 .
.
Для анализа запишем матрицу этой квадратичной формы и применим критерий Сильвестра.
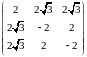
Выпишем главные миноры:
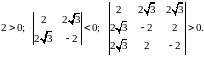
Распределение знаков миноров показывает, что данная квадратичная форма знакопеременная, таким образом в точке функция не имеет экстремума, то есть - седловая точка функции .
Аналогичным
образом определяется, что и точки
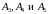 также являются Седловыми точками функции
.
также являются Седловыми точками функции
.
Задача №5:
Исследовать
на экстремумы функцию
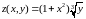 .
.
Решение:
Имеем,
что
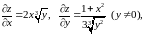 следовательно ни одна точка вне оси
следовательно ни одна точка вне оси
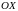 не будет критической.
не будет критической.
Пусть
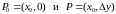 ,
тогда
,
тогда
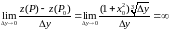
Таким
образом, все
точки оси
являются критическими точками функции
 ,
в которых
,
в которых
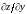 не существует. Из определения
не существует. Из определения
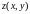 получаем, что если
получаем, что если
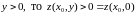 ,
если же
,
если же
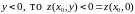 для любого
для любого
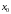 .
Итак, получается, что каждая точка на
оси
является критической точкой функции
,
и в каждой из них нарушены условия
гладкости и эти точки, следовательно,
являются седловыми точками функции
.
.
Итак, получается, что каждая точка на
оси
является критической точкой функции
,
и в каждой из них нарушены условия
гладкости и эти точки, следовательно,
являются седловыми точками функции
.
Замечание: Из примера видно, что если в критической точке функция может не иметь даже хотя бы одной частной производной, и, следовательно, эта точка может быть равновероятно точкой локального минимума, локального максимума или седловой точкой.
Задача №6:
Исследовать
на экстремумы функцию
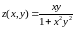 .
.
Решение:
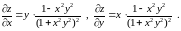
Отсюда
делаем вывод, что критическими точками
функции
будут
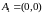 и все другие
и все другие
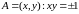 .
Из неравенства
.
Из неравенства
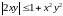 получаем, что
получаем, что
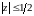 .
В каждой точке линии
.
В каждой точке линии
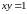 имеем, что
имеем, что
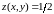 ,
а также, если
,
а также, если
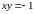 ,
то
,
то
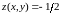 .
Таким образом можно утверждать, что в
каждой точке
функция имеет нестрогий максимум, а в
- нестрогий минимум. Найдем вторые
частные производные функции
.
.
Таким образом можно утверждать, что в
каждой точке
функция имеет нестрогий максимум, а в
- нестрогий минимум. Найдем вторые
частные производные функции
.
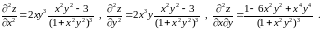
Если
,
то квадратичная форма
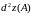 полуопределена, как и должно быть в
точках нестрогого экстремума:
полуопределена, как и должно быть в
точках нестрогого экстремума:
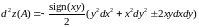 .
.
А
для точки
квадратичная форма
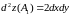 - знакопеременная, следовательно,
-
седловая точка функции
.
- знакопеременная, следовательно,
-
седловая точка функции
.
Задача №7:
Найти
точки условного экстремума функции
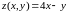 ,
если
,
если
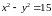 .
.
Решение:
В
этом задании
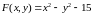 ,
матрица
,
матрица
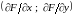 есть
есть
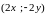 .
Из условия
следует, что все точки, удовлетворяющие
данному условию, имеют ненулевые
координаты, а значит и минор
.
Из условия
следует, что все точки, удовлетворяющие
данному условию, имеют ненулевые
координаты, а значит и минор
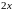 матрицы
также отличен от нуля. Поэтому условие
определяет на этом множестве функцию
матрицы
также отличен от нуля. Поэтому условие
определяет на этом множестве функцию
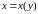 .
.
А
теперь мы рассматриваем функцию
,
как функцию одного аргумента
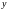 :
:
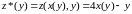 .
Из условия получаем, что
.
Из условия получаем, что
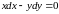 откуда
откуда
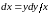 ,
подставляя, получим
,
подставляя, получим
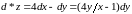 .
В итоге для координат критической точки
функции
.
В итоге для координат критической точки
функции
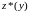 имеем систему уравнений:
имеем систему уравнений:
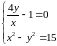
Решая
систему, получим, что возможными точками
локального экстремума могут быть точки
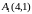 и
и
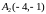 .
.
Теперь
рассмотрим
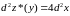 в этих точках, из условия имеем
в этих точках, из условия имеем
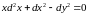 .
Тогда для
имеем
.
Тогда для
имеем
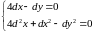 ,
,
откуда
получим, что
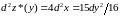 и точка
является точкой локального условного
минимума функции
при условии
,
причем
и точка
является точкой локального условного
минимума функции
при условии
,
причем
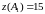 .
.
Точно
также получим, что в точке
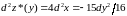 , то есть эта точка является локальным
условным максимумом функции
при условии
,
причем
, то есть эта точка является локальным
условным максимумом функции
при условии
,
причем
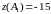 .
.
Задача №8:
Найдем
экстремальные значения функции
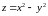 на прямой
на прямой
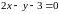 .
.
Решение:
Запишем функцию Лагранжа
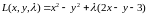
Координаты
критических точек функции
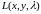 находятся из системы
находятся из системы
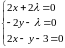

отсюда
получаем
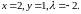 В точке (2,1,-2) выражение
В точке (2,1,-2) выражение
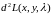 ,равное
,равное
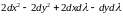 ,
есть знакопеременная квадратичная
форма, следовательно, точка (2,1,-2) не
экстремальная точка функции
,но эта точка может быть экстремальной
точкой функции
при условии связи. В самом деле, из
условия связи имеем
,
есть знакопеременная квадратичная
форма, следовательно, точка (2,1,-2) не
экстремальная точка функции
,но эта точка может быть экстремальной
точкой функции
при условии связи. В самом деле, из
условия связи имеем
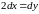 .
Учитывая это соотношение, для
.
Учитывая это соотношение, для
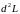 получаем выражение
получаем выражение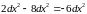 ,которое
есть отрицательно определенная
квадратичная форма, и, следовательно,
точка (2,1) является точкой локального
максимума функции
при условии связи
,которое
есть отрицательно определенная
квадратичная форма, и, следовательно,
точка (2,1) является точкой локального
максимума функции
при условии связи
ВОПРОСЫ К ЭКЗАМЕНУ.
Понятие первообразной функции и неопределённого интеграла. Свойства неопределённого интеграла.
Интегрирование путём замены переменных.
Метод интегрирования по частям.
Интегрирование выражений, содержащих квадратный трёхчлен.
Рациональные дроби. Простейшие дроби 1-4 типов, схема интегрирования дробей 1-4 типов.
Разложение правильной рациональной дроби на сумму простейшие дробей.
Метод неопределённых коэффициентов. Схема интегрирования рациональной дроби.
Интегрирование тригонометрических выражений вида
 с помощью универсальной тригонометрической
подстановки.
с помощью универсальной тригонометрической
подстановки.
Частные приращения, полное приращение Ф2П. Частные производные Ф2П.
Полный дифференциал Ф2П.
Производная по направлению, градиент функции.
Уравнения касательной плоскости и нормали к поверхности.
Определение экстремума Ф2П (локального экстремума). Необходимое условие экстремума Ф2П. Достаточное условие экстремума Ф2П.
Нахождение наибольшего, наименьшего значений Ф2П в замкнутой ограниченной области (глобальные экстремумы).
Формула Тейлора для ФМП.
