Примеры
Задача 1.Вычислить интеграл:
.
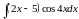Решение: применяя интегрирование по частям, получаем
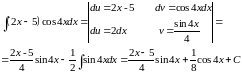
Задача №2:
Вычислить
интеграл: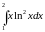
Решение:
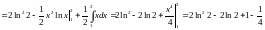
Задача №3:
Вычислить
интеграл: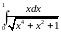
Решение:
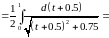
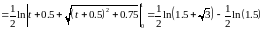
Задача №4:
Вычислить
интеграл: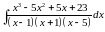
Решение:
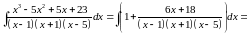
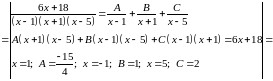
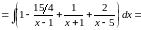
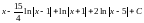
Задача №5:
Вычислить
интеграл: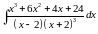
Решение:
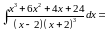
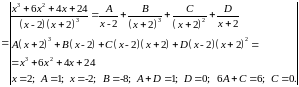
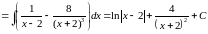
Задача №6:
Вычислить
интеграл: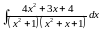
Решение:
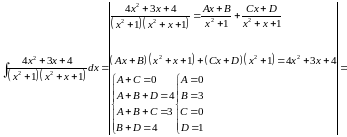
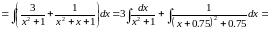
Задача №7:
Вычислить
интеграл: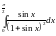
Решение:
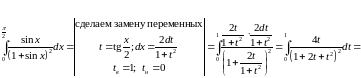
Задача №8:
Вычислить
интеграл: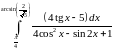
Решение:
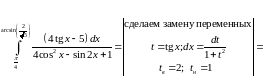
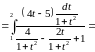
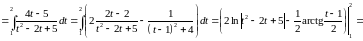
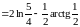
Задача №9:
Вычислить
интеграл: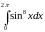
Решение:
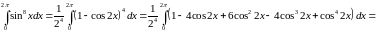
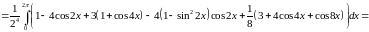
Задача №10:
Вычислить
интеграл: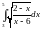
Решение:
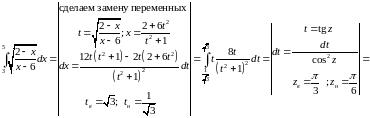
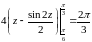
Задача №11:
Вычислить
интеграл:
Решение:
Задача №12:
Вычислить
интеграл: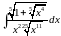
Решение:
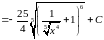
Функции многих переменных Частные производные. Геометрическая интерпретация частной производной.
Пусть
функция
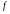определена
в некоторой окрестности точки
.
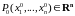Функция
называется дифференцируемой
по
,
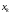если существует предел разностного
отношения
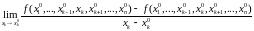(5.1)
этот
предел называется частной
производной функции
(по
)
в точке
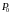и обозначается
или
.
Таким
образом, частная производная функции
равна обыкновенной производной функции
действительного переменного
,
которая получается из
,
если переменные
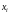для
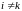положить
равными
.
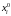Для
нахождения производной более высоких
порядков, например порядка
,
применяется специальная формула (5.2).
Эта формула получается в результате
индукции при рассмотрении частных
производных более низкого порядка.
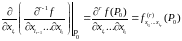(5.2).
Теоремы о дифференцируемых фмп.
Дифференцирование сложной функции.
Пусть
дифференцируема в точке
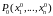и пусть
–
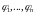функции одного переменного, дифференцируемые
в точке
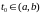и
такие, что
,
.
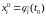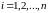Тогда сложная функция, составленная из
и
дифференцируема в точке
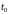и её производная находится по формуле
(5).
Экстремумы фмп.
Пусть
функция
определена в некоторой области
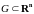и
-
точка в
.
Значение функции
в данной точке называется минимумом
(локальным
минимумом)
функции
в
,
если существует окрестность точки
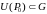точки
,
такая что для всех точек
\
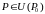выполняется неравенство
.
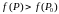Аналогично максимумом
(локальным
максимумом)
функции
в
,
если
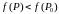. Если неравенства строгие, то локальным
максимумом (минимум) называют строгим,
в противном случае – нестрогим.
Максимум или минимум также называют
экстремумом
( локальным
экстремумом)
функции
в
.
Необходимые условия существования экстремума.
Если
-
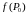экстремум функции
,
дифференцируемой по каждой из координатв
некоторой окрестности
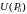точки
,
то выполняются равенства
.
Достаточные условия существования экстремума.
Пусть
функция
дважды непрерывно дифференцируема в
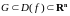и в точке
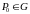выполняются равенства
.
Если, кроме того, положительно (или
отрицательно) определена квадратичная
форма
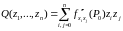(5.11)
то
функция
имеет минимум (или максимум) в точке
,
а если форма
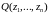неопределенная, то функция
не имеет экстремума в точке
и точка в этом случае называется седловой
точкой
функции
.
Нахождение условных экстремумов (метод неопределенных множителей Лагранжа).
Общая постановка задачи:
Найти
все экстремумы и наибольшее, а также
наименьшее значения функции
,
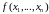определенной в области
,
для точек
,
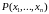удовлетворяющих дополнительным
условиям:
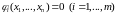(5.12)
где
-
действительные функции, определенные
в
.
Необходимые условия существования условного экстремума.
Пусть
функции
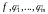непрерывно дифференцируемы в
и ранг функциональной матрицы
равен
.
Положим, что
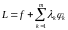(5.13)
(функция
является функцией Лагранжа с множителями
-
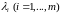произвольные действительные числа).
Если
в точке
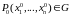при дополнительных условиях (5.14) имеет
экстремум, то справедливы соотношения:
а)
(5.14)
б)
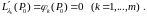
Таким
образом, необходимым условием существования
условного экстремума функции
в точке
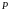при дополнительных условиях
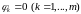являются следующие
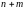уравнений с
количеством переменных
и
:
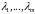(5.15)
