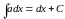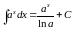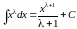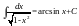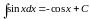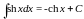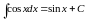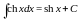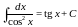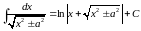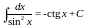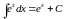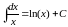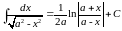Дифференциальное исчисление функции двух переменных
Задание
1. Для
функции двух переменных
,
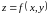пользуясь правилами дифференцирования,
найти производные:
.
№ |
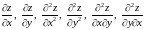Функция |
№ |
Функция |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
31 |
|
32 |
|
33 |
|
34 |
|
35 |
|
36 |
|
37 |
|
38 |
|
39 |
|
40 |
|
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
Задание 2.Найти точки экстремума функции . Характеризовать их тип.
№ |
Исследуемая функция |
№ |
Исследуемая функция |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
31 |
|
32 |
|
33 |
|
34 |
|
35 |
|
36 |
|
;
;
;
;
;
;
;
;
;
;
;
,
(
);
;
;
;
;
;
;
;
;
;
;
;
;
;
;
,
;
;
;
;
,
;
;
;
;
;
;
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ.
Таблица простейших интегралов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Геометрические приложения определенного интеграла
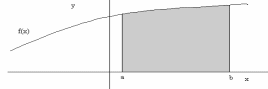
Площадь криволинейной трапеции
Площадь
фигуры, называемой криволинейной
трапецией, лежащей под графиком
и неотрицательной на отрезке
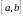равна
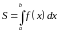
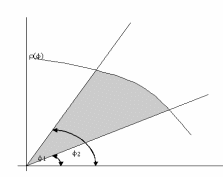
Площадь криволинейного сектора
Площадь
фигуры, называемой криволинейным
сектором, ограниченной графиком
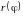и двумя лучами, составляющими с полярной
осью углы
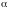и
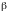имеет площадь
Вычисление объема вращения
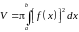
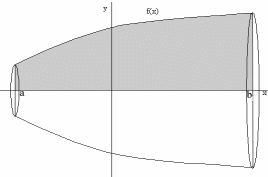
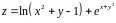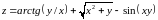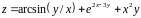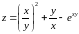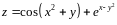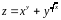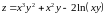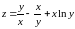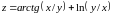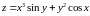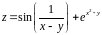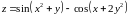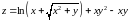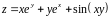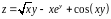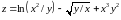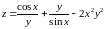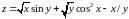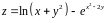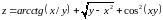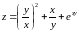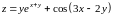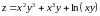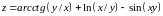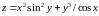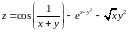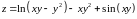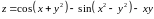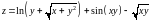
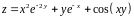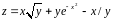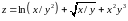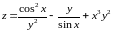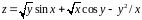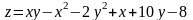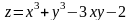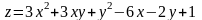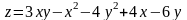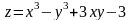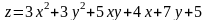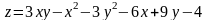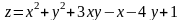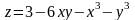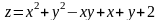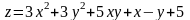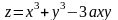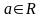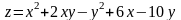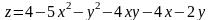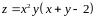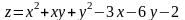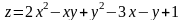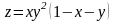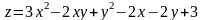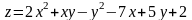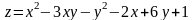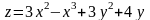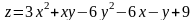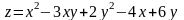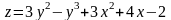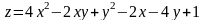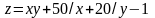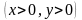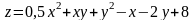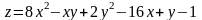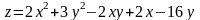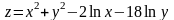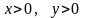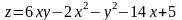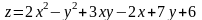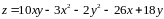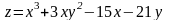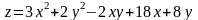